政华教育

【答案】A【解析】题目给出明显的等量关系，用方程表示出来，设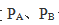分别表示A、B机器的效率，则有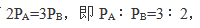据此设A、B机器的生产效率分别为3和2。根据“A和B机器一同生产3天完成了全部零件的一半”可知，两台机器一同生产3×2=6天可完成全部。当两台机器一同生产4天后，剩余零件的工作量为(3+2)×(6-4)=10，由B机器单独生产还需要10÷2=5天。故该题选A。

例题2

一批口罩的加工任务，甲单独加工12天完成。若甲先单独加工3天，再由乙单独加工2天，则能完成任务的一半。现甲和乙合作加工若干天后，再由乙单独加工至完成任务，最终发现甲、乙合作加工的时间与乙单独加工的时间相同，则完成该加工任务共用多少天？

A.3 B.4 C.6 D.8

【答案】C【解析】题目给出甲单独完工和甲乙各做一段时间的完工方式，根据题意，工作总量不变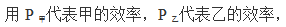，则：设甲和乙的工作效率分别是2和3，则工作总量为12×2=24。设甲、乙合作加工的时间与乙单独加工的时间都是t天，则(2+3)×t+3t=24，解得t=3，故完成该加工任务共用2×3=6天。故本题选C。

以上两题都是间接给出效率比，但是大部分同学一眼识别不出来，但能够清晰地找到等量关系，可先列出方程，化简后就可以得到效率比，再设特值，题目就会迎刃而解。望大家能认真投入，进行大量题目训练，从而拿下这一类题型。

学会特值法，行测多者合作类工程问题不再难解

行测数量关系题目一直被考生认为比较难的部分，甚至很多考生会放弃数量关系题目，其实数量关系题目也没有考生所认为的这么难。只要考生在备考过程中能够熟练掌握一些高频考点的出题规律及做题方法，部分数量关系题目还是能够又快又准地解出来的。而多者合作类工程问题就是出题规律容易掌握、做题方法可以学会、在考场上能够在较短的时间内解出的题目，并且多者合作类工程问题也几乎是每年必考的题目。

工程问题主要是研究工作总量、工作效率、工作时间三者之间关系的题。

基本公式：工作总量=工作效率×工作时间。

核心公式：工作总量=工作效率×工作时间(W=P×t)

例题1

要折叠一批纸飞机，若甲单独折叠要半个小时完成，乙单独折叠需要45分钟完成。若两人一起折，需要多少分钟完成？

A.10 B.15 C.16 D.18

【答案】D【解析】此题题干中工作效率及工作总量均未知，只知甲、乙两人单独完成工作任务所用时间，则可将工作总量设成甲、乙两人单独完成工作任务所用时间的最小公倍数，即工作总量为30和45的最小公倍数90。工作总量设定后可求甲的工作效率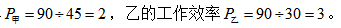则甲乙二人合作所用时间为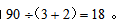也就是甲乙二人合作所需时间为18分钟。故此题应选D。

小结1：已知多个工作主体完工时间，将工作总量设为多个完工时间的最小公倍数。

例题2

甲工程队与乙工程队的效率之比为4∶5，一项工程由甲工程队先单独做6天，再由乙工程队单独做8天，最后由甲、乙两个工程队合作4天刚好完成，如果这项工程由甲工程队或乙工程队单独完成，则甲工程队所需天数比乙工程队所需天数多多少天？

A.3 B.4 C.5 D.6

【答案】C【解析】此题题干中工作总量及各自工作时间均未知，且无甲乙两队单独完成工作任务所需时间，这时可根据题干中已知的甲乙两队的效率比将两队各自的工作效率设为特值。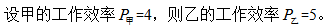则工作总量乙工程队所需时间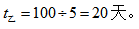所以甲工程队单独完成所需时间比乙工程队单独完成所需时间多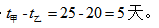故此题应选C选项。

小结2：已知多个工作主体工作效率比，将各自工作效率设为最简比对应的份数。

总结

若题干中已知多个工作主体不同的完工时间，可按照例1中设特值的方法将工作总量设为多个完工时间的最小公倍数，进而求出各自工作效率，再根据题干所问利用基本公式求解；若题干已知多个工作主体效率比，可根据例2中设特值的方式，将效率比所对应的份数设为各自工作效率，再根据题干所问进行逐步求解。

特殊题型

1.给出完工时间型

(1)题型特征：题目中已知多个主体的完工时间，问题也求时间。

(2)解题方法：可设工作总量为“1”或完工时间的公倍数，之后算出各主体的效率。

例题1

有一项工作，甲单干需要10个小时完成，乙单干需要12个小时完成。甲、乙两人同时工作5小时后，甲另有其他的事情去做，只有乙继续工作，那么完成这项工作共用了( )小时。

A.5 B.6 C.7 D.8

【答案】B【解析】方法一：设工程总量为1，则甲的工作效率为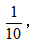乙的工作效率为甲、乙两人合作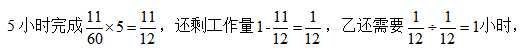完成这项工作共用5+1=6小时。本题选择B项。

方法二：假设总工作量为60(10和12的最小公倍数)，则甲的工作效率是6，乙的工作效率是5，合作5小时后还剩工作量60-(6+5)×5=5，乙还需工作1小时，所以完成这项工作共用5+1=6小时，本题选择B项。

2.给出效率关系型

(1)题型特征：题目中已知多个主体效率比或者可推导出效率间的关系。

(2)解题方法：根据效率的比例关系设效率为最简比的数值。

例题2

甲工程队与乙工程队的效率之比为4：5，一项工程由甲工程队先单独做6天，再由乙工程队单独做8天，最后由甲、乙两个工程队合作4天刚好完成，如果这项工程由甲工程队或乙工程队单独完成，则甲工程队所需天数比乙工程队所需天数多：

A.3天 B.4天 C.5天 D.6

【答案】C【解析】设甲、乙工作效率分别为4、5，则这项工程的任务量为4×6+5×8+(4+5)×4=100。甲工程队单独完成需要100÷4=25天，乙工程队单独完成需要100÷5=20天，所求为25-20=5天，故本题选择C项。

3.多个主体效率相同型

(1)题型特征：题目中已知多个主体的效率相同时。

(2)解题方法：一般设主体的效率为“1”。

例题3

修一条公路，假设每人每天的工作效率相同，计划180名工人1年完成工作4个月后，因特殊情况，要求提前2个月完成任务，则需要增加工人多少名？

A.50 B.65 C.70 D.60

【答案】D【解析】设每名工人每月的工作量为1，则全部工作量为180×12，工作4个月完成工作量180×4。设要想提前2个月就需要增加工人x名，则可得180×4+(180+x)×(12-4-2)=180×12，解得x=60。故选D。

在行测工程问题中用这类特值思想，会使我们的解题变得相对简单，计算变得相对简捷。所以，熟练地掌握以上这三种设特值的方法，是求解出“多者合作”问题的前提，考生们还需勤加练习！

行测趣味问题：他今年到底几岁

对于行测数量关系，你是否还停留在听天由命的阶段？遇到年龄问题，很多考生要么没思路，要么计算过程丢三落四。其实，要想做好年龄问题，关键点在于把握年龄差不变原则，除此之外，我们也可以尝试代入选项。今天就带着大家一起来解决年龄问题。

年龄问题常见题型

例题1

甲、乙两人今年的年龄和正好是60岁，甲对乙说：“我像你这么大时，你的年龄正好是我年龄的一半。”甲今年多少岁？

A.32 B.34 C.35 D.36

【答案】D【解析】根据题意，甲、乙两人今年年龄和为60岁，而甲、乙分别为多少岁我们并不知道，不妨设甲今年x岁，乙为60-x岁。在某年，甲像乙今年60-x这么大时，乙为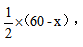根据两个人年龄差不变，可得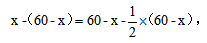整理可得x=36，即甲今年36岁，所以答案选择D。

例题2

在1999年时，小明的生日已经过了，他现在的年龄正好是他出生年份的四个数字之和，小明是哪年生的？

A.1974 B.1975 C.1976 D.1977

【答案】C【解析】该题可以代入选项，排除错误选项。首先选择一个中间选项代入，代入B，如果他是1975年出生，则1999年他的年龄为1999-1975=24岁，而此时算出他出生年份的四个数字之和为22，此时年龄比四个数字之和大，不符合题目要求。同时，A选项在B选项之前，此时得出年龄更大，但四个数字之和更小，不符合要求。1975年年份较小，所以再去验证比1975年份大的。验证C选项，如果他是1976年出生，则1999年他的年龄为1999-1976=23，而他出生年份的四个数字之和也为23，答案选择C。

通过这两个例题，大家对年龄问题有了大体的了解，当题目中出现多人在不同阶段的年龄或者年龄之间的关系，我们可以根据不同阶段这几个人的年龄差保持不变来解题。如果题目给出的条件比较少，我们也可以将选项带入，再结合年龄差不变的原则去解题。

今后大家再碰到年龄问题，可以根据年龄差不变原理去解题，这样的话解题将会容易一些。