巧解行测数量关系题

行测排列组合之如何区分“A”与“C”

排列组合问题是行测考试中的一个常客。对于很多考生来说，往往一道题不易分辨出该用排列“A”还是组合“C”，想要理解其含义，建议大家首先还是要从排列组合的基本概念入手。

一、排列组合的基本概念

排列和排列数：从n个不同元素中取出m(m≤n)个元素排成一列，记做。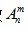

组合和组合数：从n个不同元素中取出m(m≤n)个元素组成一组，记做。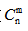

二、排列和组合的区别

从选出的几个元素中，任取两个，交换顺序，若结果不同，是排列，否则是组合。

三、对比区分排列组合

例1

四名优等生保送到三所学校去，每所学校至少得一名，则不同的保送方案的总数是_________。

错解分析：

根据题目要求每所学校至少接纳一位优等生，常采用先安排每学校一人，而后将剩的一人送到一所学校，故有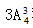种。此种办法是将同在一所学校的两名学生按进入学校的前后顺序，分为两种方案，而实际题目中对进入同一所学校的两名学生是无顺序要求的，所以此种解法错误。

技巧与方法：

解法一，采用处理分堆问题的方法。

解法二，分两次安排优等生，但是进入同一所学校的两名优等生是不考虑顺序的。

解法一：分两步：先将四名优等生分成2，1，1三组，共有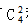种；而后，对三组学生安排三所学校，即进行全排列，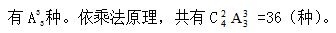

解法二：分两步：从每个学校至少有一名学生，每人进一所学校，共有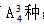；而后，再将剩余的一名学生送到三所学校中的一所学校，有3种。值得注意的是：同在一所学校的两名学生是不考虑进入的前后顺序的。因此，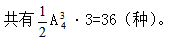

四、例题精讲，把握排列和组合

例2

有3名男生，4名女生，在下列不同要求下，求不同的排列方法总数。

(1)全体排成一行，其中甲只能在中间或者两边位置。

(2)全体排成一行，其中甲不在最左边，乙不在最右边。

(3)全体排成一行，其中男生必须排在一起。

(4)全体排成一行，男、女各不相邻。

(5)全体排成一行，男生不能排在一起。

(6)全体排成一行，其中甲、乙、丙三人从左至右的顺序不变。

(7)排成前后二排，前排3人，后排4人。

(8)全体排成一行，甲、乙两人中间必须有3人。

【解析】(1)利用元素分析法，甲为特殊元素，故先安排甲左、右、中共三个位置可供甲选择。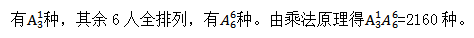

(2)位置分析法。先排最右边，除去甲外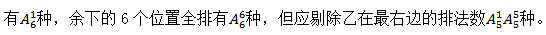，则符合条件的排法共有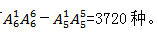

(3)捆绑法。将男生看成一个整体，进行全排列。再与其他元素进行全排列。共有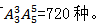

(4)插空法。先排好男生，然后将女生插入其中的四个空位，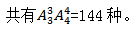

(5)插空法。先排女生，然后在空位中插入男生，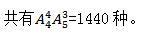

(6)定序排列。第一步，设固定甲、乙、丙从左至右顺序的排列总数为N，第二步，对甲、乙、丙进行全排列，则为七个人的全排列，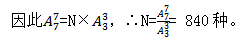

(7)与无任何限制的排列相同，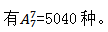

(8)从除甲、乙以外的5人中选3人排在甲、乙中间的排法有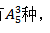甲、乙和其余2人排成一排且甲、乙相邻的排法有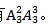最后再把选出的3人的排列插入到甲、乙之间即可。共有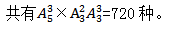

行测排列组合问题之插空法

排列组合问题中还有有很多解题的技巧，如果熟练掌握了再加以练习，可以在短时间内迅速解决的。

例如：现在有5名男生和3名女生站成一排，若3名女生彼此不能站在一起，一共有多少种不同的站法？

一、这是一道非常典型的排列组合问题，且要求元素不能相邻的题目：“3名女生彼此不能站在一起”。

二、解题方法：插空法。

即先对没有要求的元素进行排列，因此已排好的元素之间会产生空位，再将不相邻元素随机地放在空位中，这种方法就是插空法。

例题

现在有5名男生和3名女生站成一排，若3名女生彼此不能站在一起，一共有多少种不同的站法？（  ）

A.10300 B.12100 C.14400 D.15400

【答案】C【解析】首先从问题入手，问有多少种不同的站法，也就是在问有多少种方法数、情况数、结果数，即是一类计数问题，用排列组合进行解决。题目中要求3名女生彼此不能站在一起，也就是女生不能相邻。为了使女生不相邻，可以先安排男生的位置，排好男生后男生和男生之间会产生空位，再将女生安排在不同的空位上，那么女生彼此之间就不会相邻了。按照这样的思路：首先考虑男生的位置情况，5名男生排成一排，谁在前谁在后改变顺序后对应的位置发生了改变，5名男生排好之后会产生6个空位，从6个空位中选3个不同的空位放3名女生，此时不同的女生排在前后情况不同，因此要考虑顺序要求用排列进行计算，记为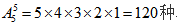不同情况。5名男生排好之后会产生6个空位，从6个空位中选3个不同的空位放3名女生，此时不同的女生排在前后情况不同，因此要考虑顺序要求用排列进行计算，记为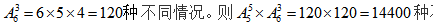不同的情况。

总结：掌握排列组合问题中元素不能相邻的解题方法插空法，即将其他元素先排列好，再将不相邻元素放在空位中。在不同的题目可能会有细微的变化，认真分析题意，如果元素均相同，则不需要排序。多加练习，快速辨析这类题型，从而达到快速求解的目的。

行测数量关系：巧解年龄问题

年龄问题在一些行测考试当中会出现，许多同学在练习的过程中不知道该如何入手，对于年龄问题所给出复杂的数据关系感觉混乱，无法整理出较为明确的关系，导致做题时没有很好的思路，但其实只要掌握了相应的解题技巧以及多加练习，就能很轻松地解决年龄问题。

年龄问题的一个重要解题原则就是任何两人年龄差保持不变，那具体如何运用到题目当中，我们一起来学习一下。

例题1

陈红今年13岁，她的母亲32岁，则（  ）年后，陈红母亲的年龄是陈红的2倍？

A.4 B.5 C.6 D.7

【解析】今年陈红和母亲的年龄差值为19岁，当母亲年龄是陈红的2倍时，母亲比陈红的年龄多1倍，差值仍然为19岁，即陈红年龄此时为19岁，再过19-13=6年。

例题2

当张叔叔是李叔叔现在的年龄时，李叔叔20岁；当李叔叔是张叔叔现在的年龄时，张叔叔35岁，那么：（  ）

A.李叔叔比张叔叔大20岁 B.张叔叔比李叔叔大20岁

C.张叔叔比李叔叔大5岁  D.李叔叔比张叔叔大5岁

【解析】方法一：设张叔叔的年龄为x，李叔叔年龄为y，当张叔叔年龄为y时，李叔叔的年龄是20，当李叔叔年龄为x时，张叔叔是35，根据年龄差不变，可列的等式有y-20=35-x=x-y，解得x=30(岁)，y=25(岁)，选择C项。

方法二：根据年龄差不变，可画出如下图的线段，可以算出每一个小线段代表的差值是5，故张叔叔比李叔叔大5岁。

例3

张老师家四代同堂，且从父亲、张老师、儿子到孙子，每两代人的年龄差的相同。5年前张老师父亲的年龄是儿子的3倍，8年后张老师的年龄是孙子的5倍。问今年四个人的年龄之和为：（  ）

A.168 B.172 C.176 D.180

【解析】根据题意，可假设5年前儿子年龄为x，则父亲年龄为3x，根据年龄差相同可知，父亲、张老师、儿子、孙子的年龄差均为x，则此时张老师的年龄为2x，孙子年龄为0。又根据“8年后张老师的年龄是孙子的5倍”，可知8年后张老师的年龄为2x+13，孙子为13岁，有2x+13=5×13，解得x=26，则今年四人的年龄和为6x+20，即6×26+20=176(岁)。

总结 

我们把常见年龄问题给大家展示出来，总的来说就是根据年龄差不变的核心原则，利用未知数表示出年龄间的关系。大家可以多去练习相关题目，提升对知识点的熟练与运用，攻破年龄问题的难关。

行测数量关系：走进“鸡兔同笼”的世界

纵观近几年行测数量关系考试题型，我们可以发现考查最多的是“计算问题”。就“计算问题”而言，分别考察了整除、比例、鸡兔同笼、不定方程、周期循环、等差数列、分段计算、十字交叉等。这些内容都是数量关系中最基本的知识点，需要各位同学对此有一定了解。今天带大家走进“鸡兔同笼”的世界，来梳理一下鸡兔同笼题型的特点和做题方法。

何谓鸡兔同笼

在《孙子算经》中有这样的记载：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？

题干告诉我们鸡兔的头的总量和脚的总量，求鸡兔各有几只。在这其中，其实还隐含了一只鸡有一头两脚，一只兔有一头四脚。所以我们可以得出鸡兔同笼问题的题型特征：已知两个主体(鸡、兔)两种属性(头、脚)的指标数(鸡1头2脚，兔1头4脚)和指标总数(35头，94脚)，分别求两个主体各有多少。所以只要是符合这样题型特征的题目都可以归为鸡兔同笼问题。

鸡兔同笼求解方法

例题

今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？

解法一：使用方程法求解。设兔有x只，则鸡有(35-x)只。则：4x+2(35-x)=94，解得x=12，即兔有12只，则鸡有：35 - 12 = 23 只。

解法二：使用假设法求解。假设笼子里的全部是鸡，则计算足，共2×35=70。实际题目说到，足有94，明显我们的假设计算少了。分析少的原因，由于每只兔子有4足，按照假设计算，每一只兔子少算了4-2=2足。总共少94-70=24足，则24÷2=12只兔子，即鸡有35-12=23只。

对比两种方法会发现，假设法直接规避了设未知数求解的过程，计算过程会更加简便。即：(1)先全部假设成一个对象；(2)再利用总盈亏÷每份盈亏=份数进行求解，求解出来的份数就是另一个对象的个数。

接下来我们再来熟练应用一下假设法解决鸡兔同笼问题的操作步骤。

例1

有一辆货车运输2000只玻璃瓶，运费按到达时完好瓶子数目计算，每只2角，如有破损，破损一只还要倒赔2角，结果得到运费393.2元，破损只数是：（  ）

A.17 B.24 C.34 D.36

【答案】A【解析】假设2000只玻璃瓶是完好的，则可以得到2000×0.2=400元，但实际得到了393.2元，少得了400-393.2=6.8元(总盈亏)；又知每损坏一只玻璃瓶就要倒赔0.2元，即共损失0.2+0.2=0.4元(每份盈亏)，所以损坏的玻璃瓶有6.8÷0.4=17只(份数)，故本题选A。

例2

某牧民饲养公羊和母羊共160只，一次共剪羊毛180斤。若每只公羊平均剪毛1斤2两，每只母羊平均剪毛8两，问：公羊比母羊多多少只？

A.120 B.100 C.80 D.75

【答案】B【解析】假设牧民饲养的全部为公羊，可以剪毛160x1.2=192斤，比实际多剪192-180=12斤(总盈亏)，一只公羊比一只母羊多剪毛1.2-0.8=0.4斤(每份盈亏)，则牧民饲养母羊12÷0.4=30只(份数)，公羊比母羊多(160-30)-30=100只，故本题选B。