政华教育

说到行测数量关系，很多同学都会存在一种畏难情绪，复习备考时不知如何入手，甚至选择放弃。其实不然，数量关系并非同学们考试拿高分的“拦路虎”，而是“垫脚石”。有些题目利用整除特性，可以快速排除选项，比起常规做法来说计算量更小，解题速度快，是同学们可以较快掌握的一类方法。今天政华教育就带大家一起来看看吧。

什么是整除？

整数a除以非零整数b除得的商正好是整数而余数是零，就说a能被b整除(或说b能整除a)，如：6÷3=2，则称6能被3整除，或3能整除6。

小数字整除如何判定？

1.局部看：

2或5，看末一位。

4或25，看末两位。

2.整体看：

整体看和：3或9，看各位数字加和能否被3或9整除。

整体看差：7或11或13，用三位截断法，数字从后往前数3位划线，用大数减小数，判断结果能否被7、11、13整除。如34567，从后往前数三位得到34和567，567-34=533，因为533不能被7整除，所以34567也不能被7整除。

3.其他合数：将合数因数分解，能同时被分解后的互质的数整除。

如何运用整除法？

想要了解整除的应用环境，就必须破解隐藏在题干中的“暗语”。通常来说，有以下两种情况：

1.文字描述的整除关系，如出现“整除”、“每”、“平均”、“倍”等字眼。

2.数据体现的整除关系，如出现分数、百分数、小数、比例时，化为最简形式后考虑整除。

例1：万圣节即将来临，哥哥给妹妹一些钱让她去买节日小装饰品。妹妹来到商店，南瓜灯18元一个，小怪兽14元一个。如果单买南瓜灯钱正好用完，如果单买小怪兽钱也正好用完。那么，哥哥给妹妹的钱数可能为：（）

A.266元 B.342元 C.459元 D.504元

【答案】D【解析】单独购买南瓜灯或小怪兽，均正好用完所有钱，说明钱数分别能被18和14整除，即钱数应能被18和14的最小公倍数126整除。代入选项中，只有D项符合。

例2：某老旧写字楼重新装修，需要将原有的窗户全部更换为单价90元每扇的新窗户。已知每7扇换下来的旧窗户可以跟厂商兑换一个新窗户。全部更换完毕后共花费16560元且剩余4个旧窗户没有兑换，那么该写字楼一共有多少扇窗户？（）

A.214 B.218 C.184 D.188

【答案】A【解析】本题常规方法可以利用窗户总数=购买数+兑换数构建方程，共买了16560÷90=184扇窗户，设总数为x，列出方程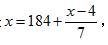解得x=214。

但本题利用整除法将更加快捷。因为窗户数只能是整数，除去未兑换的4扇窗户，其他每7扇窗户都可以换1扇新的，所以总数减去4的结果应是7的倍数。代入选项可知，只有214符合要求。该方法比方程法更加简便快速，值得一试。

政华教育相信大家学习完上述的两道题，已经对整除法在数量关系中的应用有了初步的了解。希望大家在备考的过程中多多练习，熟练地掌握利用整除解题的技巧，又快速又准确地在考试中拿到更高的分数。

行测数量关系“定位法”解决概率问题

概率问题是公职类考试中比较常见且考察比较灵活的一种题型，许多考生对于这类问题，总是一种懵懂的状态，所以，如何能在考场上把握时间快速得出答案，是大家都比较关注的。今天，政华教育带大家学习一种解决概率问题的方法：“定位法”。

例1：一张纸上画了5排共30个格子，每排格子数相同，小王将1个红色和1个绿色棋子随机放入任意一个格子(2个棋子不在同一格子)，则2个棋子在同一排的概率：（）

A.不高于15% B.高于15%但低于20%

C.正好为20% D.高于20%

【答案】B【解析】5排共有30个格子，每排格子数相同，则每排有30÷5=6个格子。总事件是从30个格子中选取2个格子分别放入两个颜色不同的棋子，样本数为所求事件是2个棋子在同一排，则可以先选择1排，再从这一排的6个格子中选取2个格子分别放入两个颜色不同的棋子，分步相乘，样本数为选择B。

以上是这种题目的常规解题思路，但是在考试过程中，这个方法却不是最快能解决这类问题的方法。要想快速解决这类问题吗，我们会用到一种方法，叫定位法。

5排共有30个格子，每排格子数相同，则每排有30÷5=6个格子。由于两个棋子相互制约，并且先放绿色还是先放红色不影响最终结果，并且第一个棋子选哪个位置，并不会影响第二个棋子的放置，所以我们可以用定位法去处理。先从30个格子中任选1个安排红色棋子，此时还剩下29个空格子。若想2个棋子在同一排，则绿色棋子只能挑选红色棋子所在排剩余5个格子中的一个，故2个棋子在同一排的概率为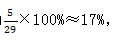选择B。

通过以上题目的解决，我们能够了解，概率问题中，在进行分组安排或位置安排时，当遇到要同时考虑两个相互制约的元素并且求两个元素处于某种特定位置的概率，可利用定位法去解决。方法是：将其中的一个元素首先固定，在此前提下，考虑另一元素的各种可能状态，从而建立相应的求解策略。需要注意的是，这种方法的应用必须满足以下两个条件：(1)一个元素先选、一个元素后选，但是无论谁先选都对最终结果不产生影响；(2)无论第一个元素选择哪个位置，也不会影响到后一个元素选择的等可能性。

例2：某学校举行迎新篝火晚会，100名新生随机围坐在篝火四周。其中，小张与小李是同桌，他俩坐在一起的概率为：（）

【答案】C【解析】题目所求为小张和小李坐在一起的概率，分析可知这两人不论谁先安排谁后安排，都对结果不产生影响，且不论第一个人坐哪个位置，都不影响后一个人选择的可能性。所以我们用“定位法”解决。小张和小李其中一人坐下之后，另一人还有99个位置可选，其中有2个位置是满足二人相邻的，则所求概率为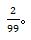

例3：某单位工会组织桥牌比赛，共有8人报名，随机组成4队，每队2人。那么，小王和小李恰好被分在同一队的概率是：（）

【答案】A【解析】假设小王已确定分队位置，小李可以选择是剩下7个位置，即总事件样本数是7个，要想和小王一队，小李可选择的只有同队的1个位置，即A事件的样本数是1个，故所求概率为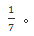

相信通过以上讲解，大家对于“定位法”解决概率问题已经不陌生，但是这种方法还是有一定的技巧性，所以大家一定要勤加练习、熟练掌握、灵活应用。

行测数量关系：怎样速解令人头痛的浓度问题？

岁岁年年，多少次答卷在公职考试中因盐水放弃；熙熙攘攘，多少位考生在行测题目中被酒精麻痹。每次看到“浓度”二字，只想绕道而行。然而，浓度问题真有那么可怕吗？恰恰相反，它正是我们可以快速拿到分数占据优势的题目之一。解决浓度问题的关键在于找对方法。

十字交叉法便是我们常用的速解浓度问题的技巧之一，这个方法本身主要是用于解决混合平均问题，即已知总体或部分的平均量，一共涉及五个量，若题中已知其中四个量，对应其位置，便可以求出五个量中的任意一个量。下面我们一起用十字交叉法来解决各类浓度问题：

例1：现有浓度为15%和30%的盐水若干，若要配出600克浓度为25%的盐水，则分别需要浓度15%和30%的盐水( )克。

A.100、500 B.500、100 C.200、400 D.400、200

【答案】C【解析】题目中给出的初始盐水浓度分别为15%和30%，混合后的浓度为25%，则可以直接用十字交叉法求出初始两种浓度盐水的用量之比，具体操作如下：

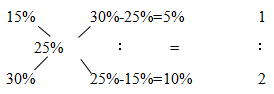
即浓度为15%的盐水和浓度为30%的盐水用量之比为1∶2，同时根据混合后盐水的质量为600克便可分别求出初始两种浓度盐水的用量，浓度为15%的盐水需要600÷(1+2)×1=200克，浓度为30%的盐水需要600÷(1+2)×2=400克。选C。

例2：小张将130克含糖5%的糖水，与含糖9%的糖水混合，配成含糖6.4%的糖水，则需要配成含糖9%的糖水( )克。

A.70 B.68 C.72 D.64

【答案】A【解析】已知，题目中给出的初始糖水浓度分别为5%和9%，混合后的浓度为6.4%，则可以直接用十字交叉法求出初始两种浓度糖水的用量之比，具体操作如下：

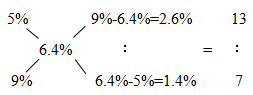
即浓度为5%的糖水和浓度为9%的糖水用量之比为13∶7，同时根据混合前浓度为5%的糖水质量为130克便可求出浓度为9%的糖水质量，故浓度为9%的糖水质量为130÷13×7=70克。选A。

例3：若要将300克浓度为95%的酒精与若干浓度为60%的酒精，混合成浓度为75%的酒精，则需要浓度为60%的酒精( )克。

A.225 B.240 C.380 D.400

【答案】D【解析】已知，题目中给出的初始酒精浓度分别为95%和60%，混合后的浓度为75%，则可以直接用十字交叉法求出初始两种浓度酒精的用量之比，具体操作如下：

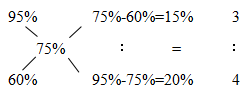
即浓度为95%的酒精和浓度为60%的酒精用量之比为3∶4，同时根据混合前浓度为95%的酒精质量为300克便可求出浓度为60%的酒精质量，故浓度为60%的糖水质量为300÷3×4=400克。选D。

以上就是我们关于十字交叉法如何速解浓度问题的详细介绍，同学们可以好好研究一些类似的题目，我们就会发现其中的共性，在今后的解题过程中拿下浓度问题也就轻而易举。

行测数量关系：和定最值里的“大”与“小”

在行测考试中，和定最值问题是考生经常遇到的题型。和定最值问题难度不高，但考生掌握的情况却不理想。那么今天就由政华教育给大家讲解如何作答和定最值问题。

题型特征

已知某几个量的和值一定，求其中某个量的最大或最小值。

解题核心

想求某个量的最大(小)值，就让其他量尽可能的小(大)。

例题展示

例1：有5人参加百分制考试，成绩总和为330分，已知5人都及格了，成绩均为整数且互不相等。

(1)成绩最好的最多得了多少分（）？

【答案】84分【解析】将5人按分数高低排成第一名至第五名。求第一名最多得了多少分，就让其他4人的分数尽可能的低。5人都及格，可知5人得分都不低于60分，又因为5人得分各不相同的整数，则第二名至第五名的分数依次为63、62、61、60分。第一名的分数=330-63-62-61-60=84分。

(2)成绩最好的最少得了多少分（）？

【答案】68分【解析】求第一名最少得了多少分，就让其他4人的分数尽可能的高。若第一名分数为x，第二名至第五名的分数依次为x-1、x-2、x-3、x-4，根据5人总分为330分，有x+x-1+x-2+x-3+x-4=330，解得x=68分。

(3)成绩排名第三的最多得了多少分（）？

【答案】68分【解析】求第三名最多得了多少分，就让其他4人的分数尽可能的低。第四名和第五名的分数分别为61、60。若设第三名的分数为x，第一名和第二名依次为x+2、x+1。有x+2+x+1+x+61+60=330，解得x=68.X。由于成绩均为整数，第三名最多得了68分。

(4)若第一名成绩不超过70分，则成绩排名第三的最少得了多少分（）？

【答案】65分【解析】求第三名最少得了多少分，就让其他4人的分数尽可能的高。第一名和第二名分数依次为70、69。若第三名分数为x，第四名和第五名依次为x-1、x-2。有70+69+x+x-1+x-2=330，解得x=64.x。由于成绩均为整数，则第三名最多得了65分。

例2：某单位2011年招聘了65名毕业生，拟分配到该单位的7个不同部门。假设行政部门分得的毕业生人数比其他部门都多，问行政部门分得的毕业生人数至少为多少名（）？

A.10 B.11 C.12 D.13

【答案】B【解析】求行政部门分得毕业人数的最小值，让其他部门分得毕业生人数尽可能的多。由题意，设行政部门分得毕业生人数为x，且题干未表述其他部门人数各不相同，其他6个部门分得毕业生人数皆为x-1，则有x+6(x-1)=65，解得x=10.x。由于分得毕业生人数为整数，则行政部门至少分得毕业生11名，选择B项。

对于和定最值问题，在平常练习时，需要注意两点：一个是排序定位的主体是否可以相同，一般是各不相同的，如果相同则在写其他数据时就需要注意一下；另一个需要注意的是最后解方程解出来的结果如果不是整数应该如何取舍，此时的取舍并非四舍五入，而是问至多则向下取整，问至少则向上取整。希望各位考生能够多加练习，掌握该题型。

行测等差数列特殊题型之“方阵”问题

在行测考试当中，有一类特殊的等差数列题型，我们把它叫做“方阵问题”。我们先来对方阵问题有一个形象认识。

我们观察上面两个图，首先我们确定点线面的关系：点通常指的是人，线就是边长，也就是每一条边的人数，面就是总人数之和。方阵其实就是一个等差数列，每一层就是一项，每一层边长之差为2，周长之差为8，这里周长之差即为方阵的公差。既然看作等差数列，那么所有关于等差数列的知识点均可用于方阵问题。当然我们也需要对方阵一些常识性的问题有个了解。

周长=边长×4-4=(边长-1)×4，为何减4？是因为四个角上的四个人被相邻的2个边重复算了1次所以减去4。

方阵核心计算注意点

1.方阵总人数=最外层每边人数的平方(面积)。

2.方阵最外层每边人数=(方阵最外层总人数÷4)+1。

3.方阵外层人数比相邻的内层人数多8人。

4.去掉m行、n列的方阵，人数减少=边长×(m+n)-mn。增加m行、n列人数也是增加这么多。立方体有6个面，6个面就是我们讨论的方阵，其是方阵的延续。计算一个立方体的元素数量就是考虑由面转为体，从面积转为体积。方体人数=边长×边长×边长(体积)方体具有的特点也就是立方体具有的特点。我们来通过一个例题来看下：

例题：学校要组织同学们参加一场广播操比赛，将学生们排成一个方阵，最外层的人数是60人，问参加这次广播操比赛共有学生多少人（）？

A.256人 B.250人 C.225人 D.196人

【答案】选A【解析】首先这题是一道典型的方阵问题，我们可以直接应用我们刚刚所学的知识。根据最外层60，可以计算出边长=60÷4+1=16，即人数16×16=256，选择A选项。

此题还可以根据方阵的基本特征来判断，方阵人数是一个平方数，锁定AC，其次，最外层是60，说明边长是一个偶数，则平方数也是偶数即选A。

我们通过例题可以看到，方阵问题本身的难度并不是很大，只要我们掌握了正确的方法，在考试有限的时间内是可以在1分钟以内做出来的。我们在平时只要针对这种题型做一些练习，把握住方阵的核心要素，再结合平方数、奇偶性等相关知识，就能快速地在考试中确定答案！