政华教育

说到行测考试中最让广大考生头疼的莫过于数量关系部分了，甚至很多考生上考场看到数量关系部分就直接跳过了，或者点兵点将随便选个答案，最后正确率全靠“天意”。但其实数量关系中有很多题都是比较容易拿分的，比如像今天我们要学习的等差数列问题，政华教育跟大家一起来探讨一下在等差数列求和时比较常用也比一般方法更为简单的一个方法：中间项求和。

什么是中间项

在等差数列中最中间的一项或者两项就叫做中间项。

例如：在等差数列1，3，5，7，9中，5就是它的中间项；

又比如在数列1，4，7，10，13，16中，7和10就是它的中间项。

常考公式

当n为奇数时，前n项和Sn=中间项×n

当n为偶数时，前n项和Sn=中间两项和×n÷2

例1：某商店10月1日开业后，每天的营业额均以100元的速度上涨，已知该月15日这一天的营业额为5000元，问该商店10月份的总营业额为多少元（）？

A.163100 B.158100 C.155000 D.150000

【答案】B【解析】每天的营业额构成公差为100的等差数列，10月共有31天，也就是说项数为31项，16日的营业额为中间项，依题意16日营业额为5000+100=5100元，根据等差数列中项求和公式，则该商店10月份的总营业额为5100×31=158100元，选B。

例2：某成衣厂对9名缝纫工进行技术评比，9名工人的得分恰好成等差数列，9人的平均得分是86分，前5名工人的得分之和是460分，那么前7名工人的得分之和是多少（）？

A.602 B.623 C.627 D.631

【答案】B【解析】9人的得分构成等差数列，且9人的平均分是86分，所以9人总分应该是86×9=774分，即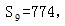中间项为第5项，根据等差数列中项求和公式可知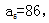即第5名工人得分为86分。同理，由前5名工人得分之和为460分，可知中间项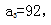，即第3名得分为92分。问题求前7名得分之和，即前7项和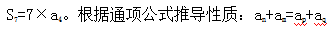(当且仅当n+m=P+q时等号成立)可知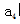即第4名得分为(92+86)÷2=89，则前7名得分之和为89×7=623分。因此选B。

通过上边的学习，我们不难发现，等差数列求和实际并不难，只要我们分析清楚题目，套用公式就可进行求解，从而得到正确选项。

行测数量关系：定位法助力解决概率问题

概率问题是行测数量关系中难度较大的一种题型。在解决概率问题时，有部分题目可以通过定位法来简化思考过程，方便计算。接下来政华教育就带着大家一起来感受定位法是如何解决概率问题的。

如果所求的问题中涉及了两个互相制约的元素，并且两个元素的选择顺序对结果没有影响，此时我们就可以把其中一个元素位置固定，再去考虑另外一个元素的位置，这种方法就叫定位法。

例1：某学校举行迎新篝火晚会100名新生随机围坐在篝火四周。其中，小张与小李是同桌，他俩坐在一起的概率为：（）

【答案】C【解析】本题所求为无论先让小张坐再研究小李的位置，还是先让小李坐再研究小张的位置，其最终结果是一样的，所以我们可以根据定位法解决这道题目。分析总事件时固定小张以后，再安排小李，一共有99个位置可以选择，所以总事件的等可能样本数是99。而在分析A事件时，固定小张以后，小李要和小张坐在一起的话，需要选择与小张相邻的左侧或右侧的位置，共有两个位置可以选择，故A事件的等可能样本数是2。所以这道题的概率是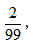选择C项。

例2：一张纸上画了5排共30个格子，每排格子数相同，小王将1个红色和1个绿色棋子随机放入任意一个格子(2个棋子不在同一格子)，则2个棋子在同一排的概率：（）

A.不高于15% B.高于15%但低于20%

C.正好为20% D.高于20%

【答案】B【解析】所求为无论先放红色棋子再放绿色棋子，还是先放绿色棋子再放红色棋子对结果没有影响，所以这道概率问题可以用定位法解决。分析总事件时固定红色棋子以后，再安排绿色棋子，有29个位置可以选择，所以总事件的等可能样本数是29。分析A事件时固定红色棋子以后，绿色棋子要和红色棋子在同一排的话，绿色棋子还有5个位置(因为一共5排30个，那么一排就是6个，当红色棋子放入后该排还剩5个位置)，即A事件的等可能样本数是5。故概率为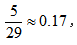选择B项。

通过以上两道题目的分析，相信大家对于定位法解决概率问题有了一定了解。政华教育希望大家能多加练习，牢牢掌握。

行测数量关系：如何确定一元二次函数的最值

在行测考试中，数量关系一直都是最不容易掌握的一种题型，但其中部分题目其实是有规律可循的，只是很多同学并不清楚。下面就由政华教育带领大家一起来学习针对一元二次函数求最值的解题方法。

对于一元二次函数而言，其图像是一条抛物线，一般在顶点位置可以取得最值。又因为图像是对称的，所以往往可以将函数式整理为两项相乘的形式，进而计算出函数式为0时的两个根，并算出两个根的平均值，这一数值就位于对称轴上，可以使得一元二次函数求得最值。

例1：某苗木公司准备出售一批苗木，如果每株以4元出售，可卖出20万株，若苗木单价每提高0.4元，就会少卖10000株。那么在最佳定价的情况下，该公司最大收入是多少万元（）？

A.60 B.80 C.90 D.100

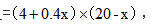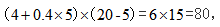【答案】B【解析】设在定价的基础上提高0.4x元，则少卖x万株，可得公司的收入因此本题所求为一元二次函数的最大值。通过列式可知，分别使得4+0.4x和20-x等于0，可以解得函数的两个根为因此最大收入会在x=5时取得，为选择B项。

例2：某汽车坐垫加工厂生产一种汽车坐垫，每套的成本是144元，售价为200元。一个经销商订购了120套这种汽车坐垫，并提出：如果每套坐垫的售价每降低2元，就多订购6套。按经销商的要求，该加工厂获得最大利润需售出的套数是( )？

A.144 B.136 C.128 D.142

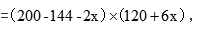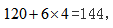【答案】A【解析】设在售价的基础上降低2x元，则多卖6x万套，可得工厂利润因此本题所求为使得一元二次函数取值最大的解。通过列式可知，分别使得200-144-2x和120+6x等于0，可以解得函数的两个根为因此最大利润会在x=4时取得，销售的套数为选择A项。

通过上面两道题目的介绍，相信大家对如何计算一元二次函数的最值问题已经有所了解。正如古语所言“宝剑锋从磨砺出，梅花香自苦寒来”，政华教育建议大家在备考期间多加练习，才能真正熟练掌握这种方法。

搞定行测利润问题，从这里着手

在行测考试中，利润问题一直备受青睐，每次考试都能看见“它”的身影。对此，也有部分同学觉得痛苦不堪，觉得利润问题是“心头病”，那如何才能解决利润问题呢？政华教育建议大家要抓住以下几点。

基本公式

基本公式在利润问题中是找等量关系的核心，因此，基本公式必须熟悉掌握。常见的基本公式有：

下边我们通过一个简单的例题来试一下。

例1：某种服装按定价出售，每件可获利90元；按定价的八五折出售20件与减价40元出售24件，所获得的利润相同。则这种服装每件成本价为多少元（）？

A.110 B.100 C.135 D.125

【答案】A【解析】根据题意，已知按八五折售20件利润与每件减价40元售24件相同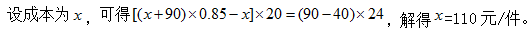，故本题选A。

题干梳理

在求解利润问题时，往往会遇到题干较长，数据较多的情况，这时候就需要对数据进行梳理，以便更好地找出等量关系列式，以简化运算，其中，梳理题干较为直观的方法为列表法，下边我们便通过一个具体的例题来学习一下。

例2：某商场销售某种商品，第一个月将此商品的进价加价20%作为销售价，共获利6000元，第二个月商场搞促销活动，将商品的进价加价10%作为销售价。第二个月的销售量比第一个月增加了100件，并且商场第二个月比第一个月多获利2000元。此商品第二个月的销售件数是：（）

A.270 B.260 C.170 D.160

【答案】D【解析】设商品单价为x元/个，根据题意梳理信息可得：

由表格可知，第一个月总利润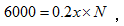第二个月总利润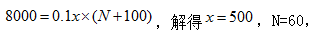故二月销量为60+100=160件。

特值简化运算

在利润问题中除了使用公式和列表，我们还会遇到一类题目，它既可以使用公式，又可以使用列表，但都不是最简单的解法，这类题目便是利润问题中的特值法。那么，使用特值法求解的题目有怎样的特点？该怎么特值呢？让我们一起来记下以下特值关系。

特点：题干中的等量关系往往以相关量的形式呈现，大部分可以使用特值法。

如何特值：特值时往往将成本、数量等特值为整十、整百、整千等，当然，也可以特值为“1”以简化运算。

例3：某水果店销售一批水果，按原价出售，利润率为25%。后来按原价的九折销售，结果每天的销量比降价前增加了1.5倍。则打折后每天销售这批水果的利润比打折前增加了（）

A.15% B.20% C.25% D.30%

【答案】C【解析】设这批水果每千克的进价为x，则原价为1.25x，设按原价销售的销量为1，总利润为0.25x；打九折后，售价为1.25x×0.9=1.125x，销量为2.5，总利润为0.125x×2.5。所求为(0.125x×2.5-0.25x)÷0.25x×100%=25%。