政华教育

【答案】B【解析】方法一：题目当中出现了两个不同的时间1995年和2018年，我们可以以此作为突破口，设1995年儿子年龄x岁，则妈妈年龄(x+26)岁，爸爸年龄(x+33)岁。根据1995年，一家三口的年龄之和为62岁，可列方程：x+x+26+x+33=62。解得：x=1。所以2018年儿子的年龄为：1+(2018-1995)=24岁。因此选B。

方法二：妈妈比儿子大26岁，爸爸比儿子大33岁。所以爸爸比妈妈大7岁。选B选项。

例2：小强的爸爸比小强的妈妈大3岁，全家三口的年龄总和是74岁，9年前这家人年龄总和是49岁，那么小强的妈妈今年多少岁（）？

A.32 B.33 C.34 D.35

【答案】A【解析】题目中提到了两个不同时间点的全家人口的年龄和，所考察的就应该是某个人因为晚出生所带来的年龄和的变化。题目告诉我们现在全家三口的年龄总和是74岁，9年前总和是49岁，即9年间3个人年龄增加了74-49=25岁。但是理论上3个人如果都增加9岁的话应该增加3×9=27岁，之所以会有所不同，就是因为有人晚出生了，而晚出生的就一定是小强了，小强晚出生了27-25=2年，也就是说今年小强的年龄应该是9-2=7岁。而问题问的是小强的妈妈今年多少岁。那么我们不妨假设妈妈今年是x岁，爸爸就是x+3岁，小强是7岁。因此x+x+3+7=74，解得x=32岁，即小强妈妈今年就是32岁，因此选A。

通过上述两道例题，相信大家对于年龄问题有了一个不错的了解。在备考练题的过程中遇到了这种类型的题目，大家就可以利用上面讲到的方法进行求解。

等量关系复杂时如何使用特值法

对于工程问题，我们需养成分析题干描述的工作方式，并结合基本公式根据明显的时间或工作量关系建立等量关系的习惯。在建立等量关系的过程中，我们习惯于设特值优化解题步骤。当遇到条件描述比较复杂的情况时，大家知道该怎么使用特值法么？接下来政华教育和大家一起来学习复杂等量关系下如何使用特值法。

当已知多个主体效率的倍数关系时，可将效率关系转化为nA=mB(A、B表示不同合作主体的效率)，设A为m，B为n。

例1：一项工程由甲、乙、丙三个工程队共同完成需要22天，甲队工作效率是乙队的3/2倍，乙队3天的工作量是丙队2天工作量的2/3。三队同时开工，2天后，丙队被调往另一工地，那么甲、乙再干多少天才能完成该工程（）？

A.20 B.28 C.38 D.42

【答案】C【解析】根据甲队工作效率是乙队的3/2倍，可设乙队的效率为2，则甲队的效率为3，设丙队的效率为x，则有2×3=x×2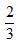，解得x=4.5。设甲、乙再干t天才能完成该工程，则有(3+2+4.5)×22=(3+2+4.5)×2+(3+2)×t，解得t=38。

根据不同工作方式的工作量相等建立等量关系后可推出，形如nA=mB(A、B表示不同合作主体的效率)的效率关系，设A为m，B为n。

例2：有一项工程甲公司花6天，乙公司再花9天可以完成，或者甲公司花8天，乙公司再花3天可以完成，如果这项工程由甲或乙单独完成，则甲公司所需天数比乙公司少多少天（）？

A.15 B.18 C.24 D.27

【答案】B【解析】用甲、乙分别表示两公司的工作效率，根据不同工作方式下工作总量不变可得，6×甲+9×乙=8×甲+3×乙，化简可得，甲=3乙，设甲=3，乙=1，则工作总量为6×3+9×1=27，甲单独完成需要27×3=9天，乙单独完成需要27×1=27天，所以甲公司所需天数比乙公司少27-9=18天。

下边我们用一道例题来检验一下大家的学习成果吧。

例3：A、B两台高性能计算机共同运行30小时可以完成某个计算任务。如两台计算机共同运行18小时后，A、B计算机分别抽调出20%和50%的计算资源去执行其他任务，最后任务完成的时间会比预计时间晚6小时。如两台计算机运行18小时后，由B计算机单独运行，还需要多少小时才能完成该任务（）？

A.22 B.24 C.27 D.30

【答案】C【解析】用A、B分别表示两台计算机的效率，则有30×(A+B)=18×(A+B)+(80%A+50%B)×(30-18+6)，化简得4A=5B，设A、B分别为5、4，则两台机器运行18小时后剩余的工作量为(30-18)×(5+4)=12×9，B单独完成需要12×9×4=27小时。

相信大家通过上述三道题目，能对复杂等量关系下如何使用特值法有所了解，政华教育建议大家在备考期间需多多练习，真正做到熟练掌握这类问题。

工程合作特值巧解

在行测备考过程中你是否有准备忍痛放弃数量的想法？有过想在数量上努力却无从下手的困境吗？其实，这大概是因为对数量不太了解而导致的，数量关系虽然涉及的知识点广阔甚至有一些难题，但是，并不是所有的数量关系都很难，工程问题就是数量关系中经常出现且易得分的类型，也是我们拿分的重点。那么今天政华教育带大家来总结一下如何解决多者合作的工程问题。

首先，我们要了解工程问题的一些基础知识。第一，工程问题基础公式为：工作总量=工作效率×工作时间，用字母表示就是W=P×T。第二，多者合作的效率等于各部分效率之和，即P合=P1+P2+P3+……+Pn

其次，我们一起来探索多者合作工程问题的题型、特征以及解题方法。常见类型有两类：

一、已知同一工程的多个完工时间，特值工作总量为时间们的最小公倍数。

“多个完工时间”有两层意思。一层是，工程必须完成，即工作总量是一定的；另一层是，在完工过程中不可改变，必须保持一个效率完成。比如下边这个例题。

例1：录入员小张和小李需要合作完成一项录入任务，这项任务小李一人需要8小时，小张一人需要10小时。两人在共同工作了3个小时后，小李因故回了趟家，期间小张一直在工作，小李返回后两个人又用了1个小时就完成了任务。在完成这项任务的过程中，小张比小李多工作了几个小时？（）

A.1 B.1.5 C.2 D.2.5

【答案】A【解析】在这道例题中，有“8小时、10小时”两个完成工作的时间，且工作中没有改变，默认保持同一效率，我们称为“多个完成时间”。那么设工作总量为8、10的最小公倍数40，则小李的效率为40÷8=5，小张的效率为40÷10=4，设小张比小李多工作T小时，则有：(4+5)×3+4T+(4+5)×1=40。解得，T=1，选择A。

二、已知或可整理出工作效率的关系，将工作效率设为最简比。

如果题目中没有出现多个完工时间，我们就可以考虑能否从题干信息中整理得到效率的比例关系，从而设工作效率为最简比。常见的工作效率关系有以下几种句式：

第一，“甲乙的效率之比为3∶4”，直接给出比例关系；

第二，“甲工作2天的量与乙工作3天的量相同”，可得到P甲：P乙=3∶2；

第三，“同一工程，甲单独做3天后，由乙继续工作4天可完成；或者甲单独做2天后，由乙继续工作6天可以完成”，由信息可得3×P甲+4×P乙=2×P甲+6×P乙，整理后得到P甲=2P乙。

下面我们通过一道例题来理解这类解题方法。

例2：一件工作甲先做6小时，乙接着做12小时可以完成；甲先做8小时，乙接着做6小时也可以完成。如果甲做3小时后由乙接着做，则还需（）小时完成。

A.16 B.18 C.21 D.24

【答案】C【解析】题目中“一件工作甲先做6小时，乙接着做12小时可以完成；甲先做8小时，乙接着做6小时也可以完成”可以得出6×P甲+12×P乙=8×P甲+6×P乙，整理可的P甲∶P乙=3∶1。所以设甲的效率为3，乙的效率为1，根据题意工作总量为6×3+12×1=30。设乙还需要T小时完成，则有，3×3+1T=30，解得T=21。选C。

这两类题型是工程问题中的常考题型，希望同学们能多加练习，同时希望同学们看到数量关系不要畏难，多多探索可以入手的题型，以达成自己的目标。

古典概率问题之定位法

众所周知，数量关系一直是行测试卷中大家比较头疼的地方，但行测要想取得好成绩，在掌握好其他部分的前提下，数量关系是得高分的关键！今天，政华教育带大家分享一下在古典概率问题中，经常会用到的定位法。在分享定位法之前，先回顾下最基本的古典概率相关知识。

基本知识

1.古典概率概念：又称“等可能事件概率”，研究的是有限个等可能事件发生的概率。

2.特征：

①基本事件数有限

②基本事件的概率相等

3.计算公式：

例1：一张纸上画了5排共30个格子，每排格子数相同，小王将1个红色和1个绿色棋子随机放入任意一个格子(2个棋子不在同一格子)，则2个棋子在同一排的概率：（）

A.不高于15% B.高于15%但低于20%

C.正好为20% D.高于20%

方法一：

(1)总事件是什么？总事件的样本数为多少？

(2)所求事件是什么？所求事件的样本数为多少？

(3)根据古典概率公式求解。

在30个格子中选出两个格子放棋子，事件数是有限个，棋子是随机放入格子的，每个格子被选择的概率是相等的，所以这符合古典概率的特征，那么可以套用公式解题。5排共有30个格子，每排格子数相同，则每排有30÷5=6个格子。总事件是从30个格子中选取2个格子分别放入两个颜色不同的棋子，放置时顺序的改变对结果有影响，所以是排列，样本数为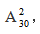所求事件是2个棋子在同一排，则可以先选择1排，再从这一排的6个格子中选取2个格子分别放入两个颜色不同的棋子，分步相乘，样本数为选择B。

运用第一种方法是套用公式的一般思路，较为繁琐，对于排列组合学得不好的同学来说比较困难，在这里和大家分享一个非常简便的方法：定位法——当遇到要同时考虑相互联系的元素时，可以先将其中一个固定，再考虑其他元素的所有可能情况，从而进行求解。

方法二：定位法求解。

题目要求两个棋子放在同一排，则这两棋子是需同时考虑且相互联系的，可以用定位法解题。5排共有30个格子，每排格子数相同，则每排有30÷5=6个格子。先从30个格子中任选1个安排红色棋子，此时还剩下29个空格子。若想再选一个格子放绿色棋子，则共有29种，但绿色棋子如果想和红色在同一排，则绿色棋子只能挑选红色棋子所在排剩余5个格子中的一个，故2个棋子在同一排的概率为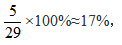选择B。

例2：某单位工会组织桥牌比赛，共有8人报名，随机组成4队，每队2人。那么，小王和小李恰好被分在同一队的概率是：（）

【答案】A【解析】分析题干可知，小王和小李要分在同一队，是需同时考虑且相互联系的，则可以用定位法。假设小王已经分好队，剩下7个位置小李可以选择，要想和小王一队，只有1个位置可选择，故两人被分在同一队的概率是1/7。

例3：某学校举行迎新篝火晚会，100名新生随机围坐在篝火四周。其中，小张与小李是同桌，他俩坐在一起的概率为：（）

【答案】C【解析】分析题干可知，小张和小李要坐在一起，是需要同时考虑且相互联系的，可以用定位法。小张和小李其中一人坐下之后，另一人还有99个位置可选，其中有2个位置是满足二人相邻的，则所求概率为2/99。

通过以上三道题目和大家分享了一下在求解古典概率问题时定位法的运用，希望大家在遇到类似题目时可以辨别出来，从而顺利解题。

表格法带你解决利润问题

利润问题是研究在经济生活中出现交易时，成本、售价、利润、利润率、打折等概念之间计算关系的一类问题，是考试的重要考点。

求解利润问题既要掌握相关概念，熟记各概念间的计算关系，还要在遇到题干信息较多时，能够借助表格梳理清楚题干信息帮助我们解题，接下来今天政华教育带你用表格解决利润问题。

例1：某商品按定价出售，每个可获得60元的利润。按定价打八折出售10个所获得的利润，与按定价每个减价30元出售15个所获得的利润相同。该商品的定价为多少元（）？

A.75 B.8O C.85 D.90

【答案】A【解析】设该商品的成本为x元，则定价为(x+60)元，所以根据题意有

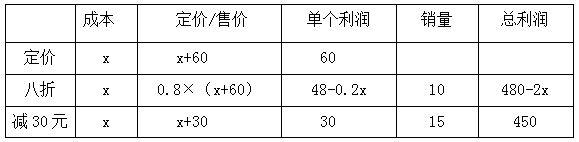
由“定价打八折出售10个所获得的利润，与按定价每个减价30元出售15个所获得的利润相同”可列方程480-2x=450，解得x=15，所以x+60=75。故本题选A。

例2：某集团旗下有量贩式超市和便民小超市两种门店，集团统一采购的A商品在量贩式超市和便民小超市的单件售价分别为12元和13.5元。4月A商品在两种门店分别售出了600件和400件，共获利5000元，问：该商品进价为多少元（）？

A.7.2 B.7.6 C.8.0 D.8.4

【答案】B【解析】设该商品进价为x元/件，所以根据题意有：

由“共获利5000元”可列方程600×(12-x)+400×(13.5-x)=5000，解得x=7.6，故本题选B。

通过上面的例题，相信大家对于如何利用表格法解决利润问题也有了一个初步的了解。政华教育建议大家备考期间需要多做题，熟练掌握利润问题中借助表格的解题方法，希望对于大家的备考能有所帮助。