政华教育

【答案】B【解析】根据题干描述，部门领导捐款总额+普通员工捐款总额=总捐款额度；设部门领导x人，普通员工y人。得出等量关系50x+20y=320，化简得：5x+2y=32，且x、y表示实际人数，皆为正整数，观察得y的系数2与常数项32有公约数2，故2y为一个可以被2整除的正整数，加上5x得到32，仍可以被2整除，故5x可以被2整除，则x必可以被2整除，正确答案B。

小结：在正整数范围内求解时，未知数系数与常数项存在非1公约数时，可用整除。

技巧二：系数一奇一偶，性质显现身手

例2：办公室工作人员使用红蓝两种颜色的文件袋装29份相同的文件，每个红色文件袋可装7份文件，每个蓝色文件袋可装4份文件，要使每个文件袋都恰好装满，需要红色、蓝色文件袋的数量分别为多少个（）？

A.1、6 B.2、4 C.4、1 D.3、2

【答案】D【解析】根据题干描述，红色文件袋所装文件数+蓝色文件袋所装文件数=文件总数，设红色文件袋用x个，蓝色y个，则有：7x+4y=29。观察两未知数系数一个奇数一个偶数，x、y表示文件袋个数都为正整数，则4y为偶数，29为奇数，一个偶数加7x得到奇数，故7x为奇数，即x为奇数，结合选项排除BC，代入A选项等式不成立排除，正确答案D。

小结：在正整数范围内求解时，未知数系数一奇一偶时，可用奇偶性。

技巧三：尾数0或5，追着个位堵

例3：有271位乘客欲乘大小两种客车旅游，已知大客车有37个座位，小客车有20个座位，为保证每位游客均有座位，且车上没有空座，则需要大客车多少（）？

A.1辆 B.3辆 C.2辆 D.4辆

【答案】B【解析】根据题干描述，大客车乘坐人数+小客车乘坐人数=总人数，设大客车x辆，小客车y辆，则37x+20y=271，x、y表示车的辆数，均为正整数。20y尾数为0，加37x得到271尾数为1，故37x尾数为1，结合选项只有B满足要求。

小结：在正整数范围内求解时，未知数系数为5或10的倍数即尾数为0或5时可用尾数法。

通过三个例题，政华教育对于不定方程三个解题技巧进行了分享，大家要想熟练掌握还需多练习、勤应用。

行测技巧：行程图——一举两得的作用

行程问题是行测考试中经常考查的一种题型，其复杂的运动过程让不少考生望而却步，掌握行程图会让行程问题变得简单明了，接下来政华教育给大家介绍行程图一举两得的作用。

作用介绍

(一)作用之一梳理题干运动过程

多数考生做行程问题的难点在于难以理解题干运动过程，而行程图可以帮助我们理清题干的运动过程。

例1：甲从某地出发匀速前进，一段时间后，乙从同一地点以同样的速度同向前进，在K时刻乙距起点30米；他们继续前进，当乙走到甲在K时刻的位置时，甲离起点108米。求乙所走过的路程。

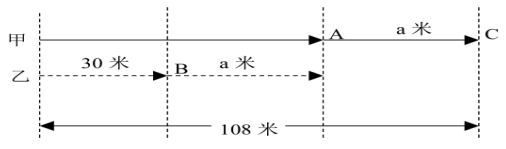
【答案】根据题意可画出下图，在K时刻，甲和乙分别在A、B两点，且相隔距离表示为a米，他们继续前进，乙从B点前进到A点，同时甲从A点前进到C点，因为两人以相同的速度匀速前进，所以A、C两点之间的距离也为a米。

这样我们使用行程图就使题干运动过程直观地展现在我们眼前，从而会使后续解题过程变得简单。

(二)作用之二构造等量关系

通过寻找行程图上线段间的等量关系，可达到最终的解题目的。如上题，根据图中线段间的关系可得30+a+a=108，解得a=39，故整个过程中乙走了30+39=69米。

实战演练

例2：甲乙两座城市相距530千米，货车和客车分别从两城出发，相向而行。货车每小时行50千米，客车每小时行70千米。客车因故比货车晚出发1小时，两车在途中某地相遇。问相遇时货车行驶多少千米（）？

A.100千米 B.150千米 C.200千米 D.250千米

【答案】D【解析】设客车出发后，经过t小时两车相遇，作图如下，则有50+50t+70t=530，解得t=4，故相遇时货车行驶了50+50×4=250千米。

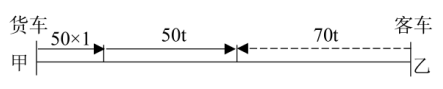
例3：某宣讲团甲宣传员骑摩托车从红星村出发以20千米/时的速度去相距60千米的八一村，1小时后由于路面湿滑，速度减少一半，在甲出发1小时后，乙宣传员以50千米/时的速度开车从红星村出发追甲，当乙追上甲时，他们与八一村的距离为：（）

A.35千米 B.30千米 C.25千米 D.40千米

【答案】A【解析】设乙从出发到追上甲所用的时间为t小时，结合题意作图如下，根据图中线段间的关系可得，20+10t=50t，解得t=0.5，所求为60-50t=35千米。

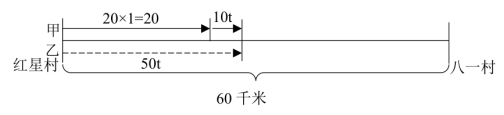
通过上面的例题，大家会发现行程图一方面帮助我们理清了运动过程，另一方面帮助我们找到了等量关系以达到最终解题的目的，可谓一举两得。政华教育建议大家备考期间多做题，熟练掌握行程图的画法，让行程图发挥最大的作用。

学会行测实战技巧，助你抓住和定最值

在往年的行测考试中，数量关系一直是广大考生备考过程中一块难啃的硬骨头。在数量关系中有一种叫做和定最值问题的题型，此类题型考查的频度相对来说比较高，且这类题型的变化多样，小白考生往往在第一次解题时无从下手。但是如果你了解了这类题型的特点，你就会发现，此类题型的难度其实是较为适中的。因此对每一位考生而言，只要学习了相应的题型特征和解题技巧，在面对和定最值问题的时候就能够做到游刃有余。今天政华教育就为广大考生分享和定最值问题这一题型，帮助大家更好地了解、吸收乃至攻克它。

首先，我们需要知道什么是和定最值问题。和定最值指的是某几个量的和一定，求其中某个量的最大值或最小值问题。

例题：已知2人的年龄互不相同且为整数，年龄之和为27。(1)问两个人中年龄最大的人年龄最大为多少岁？(2)问两个人中年龄最大的人年龄最小为多少岁？

这是典型的和定最值问题，两个人的和一定，为27，求年龄最大的人的最大值或最小值。接下来，我们一起来分析一下上面这道题目。既然两个人的年龄之和是定值，第一小题，要使年龄最大的人年龄最大，可先分析另一个人的年龄情况。为了保证最大年龄，可以让另一个人的年龄尽可能少的消耗年龄总和，也就是让另一个人年龄尽可能小，那就只能让他的年龄无限趋近于0，同时，他的年龄还必须是整数，那最极端的情况就是他的年龄为1岁，因此年龄最大的人的年龄最大值就为27-1=26岁。第二小题，要使年龄最大的人年龄最小，同理第一小题，分析另一个人的年龄情况。为保证年龄最大的人取到最小年龄，则需要让另一个人的年龄尽可能多的消耗年龄总和，即另一个人年龄尽可能大，由于他的年龄最大也不能超过年龄最大的那个人，因此只能令他的年龄无限接近年龄最大的但是又不能相等，同时，他的年龄还得是整数，那最极端的情况就是两个人年龄差1岁，假设年龄最大的年龄为x岁，那年龄小的应该为x-1。那么根据两人年龄总和为27，则有：x+(x-1)=27，解得x=14，因此年龄最大的人的年龄最小值就为14岁。

因此，不难发现和定最值的解题原则是：若求某个量的最大值，则应让其余量尽可能小；若求某个量的最小值，则应让其余量尽可能大。

接下来，让我们一起感受一下和定最值问题的几种常见考点。

(1)同向极值问题

例1：21棵树栽到5块大小不同的土地上，要求每块地栽种的棵数不同，问栽树最多的土地最多可以栽树多少棵？

【答案】要求最大量的最大值，且量各不相同，则使其他量尽可能的小且接近，即为从1开始的公差为1的等差数列，依次为1、2、3、4，共10棵，则栽树最多的土地最多种树21-10=11棵。

例2：6个整数的和为48，已知各个数各不相同，且最大的数是11，则最小数最小是多少？

【答案】要求最小数的最小值，则使其他量尽可能的大，又因为各数各不相同，那么其余5个数为公差为1的等差数列，依次为11、10、9、8、7，和为45，因此最小数最小为48-45=3。

(2)逆向极值问题

例题:现有21朵鲜花分给5人，若每个人分得的鲜花数各不相同，则分得鲜花最多的人至少分得几朵鲜花？

【答案】要使分得鲜花最多的人分得的鲜花数量最少，则要使每个人分得的鲜花数尽可能地接近。按照平均值依次分配2、3、4、5、6，正好分了20朵，还剩1朵，只能分给最多的人，因此最多的人最少分得7朵鲜花。

政华教育希望各位考生可以根据上述题目的解析，能够将和定最值问题的解题原则举一反三地应用到备考过程中遇到的和定最值题目中去。

行测数量关系：多者合作的三种特值技巧

行测备考中很多考生都会遇到一只“拦路虎”，那就是数量关系。大多数人在做这类题的时候没有掌握题型以及相应解题技巧，因此导致这个版块得分率低，这是万万不该的。数量关系其实并没有想象中那么难，只要领会常考题型以及对应的解题方法，一些题目就可以在短时间内快速解决。下面政华教育给大家介绍一种题型——工程问题之多者合作。

工程问题相信大家并不陌生，对于工程问题来说，常见的考点是多者合作。那么多者合作是什么意思呢？多者合作指的是多个主体通过一定方式合作完成某项工作。

解决多者合作问题时常将某个或多个量设为特值来简化运算，进而快速求解题目。

(1)已知多个主体完成工程的时间，可将工作总量设为单位“1”或多个完工时间的最小公倍数，进而表示出各自的工作效率；

(2)已知效率之间的比例关系时，可将效率比中的数值设为各主体效率；

(3)已知多个主体效率相同时，可将每个主体的效率为“1”。

例题1:甲、乙两队一起修一段路。甲队单独修需要8天，乙队单独修需要12天。现在两个队同时修了几天后，乙队调走，余下的路甲队在3天内修完。乙队修路的天数是：（）

A.3 B.4 C.6 D.7

【答案】A【解析】设总的工作量为24(8和12的最小公倍数)，则甲、乙的工作效率分别为3、2，甲队3天的工作量为3×3=9，所求为(24-9)÷(3+2)=3，故选A。

例题2：甲、乙、丙三人共同完成一项工作需要6小时，如果甲与乙的效率比为1∶2，乙与丙的效率比为3∶4，则乙单独完成这项工作需要多少小时（）？

A.10 B.17 C.24 D.31

【答案】B【解析】由题可知，甲、乙、丙的工作效率之比为3∶6∶8(将乙比例统一成6，故甲为3，乙为8)，则可设甲、乙、丙的工作效率分别为3、6、8，故总的工作量为(3+6+8)×6，因此乙单独完成这项工作需要(3+6+8)×6÷6=17小时。故选B。

例题3：某制衣厂有一批衣物要加工完成，假设每个工人每天的效率一样，则计划派180名工人工作12天即可完成。在工作4天后，由于特殊原因需要提前2天完成衣物的加工。问需要增加多少名工人（）？

A.40名 B.50名 C.60名 D.70名

【答案】C【解析】每个工人每天的工作效率一样，设每个工人每天的工作效率为1。根据工作总量=工作效率×工作时间，可知该项目的工作总量为180×12=2160。工作4天可完成4×180=720，截止日期提前2天，设需要增加x名工人，则有720+(180+x)×(12-2-4)=2160，解得x=60。故选C。

通过以上例题我们发现，当遇到多者合作问题时，大家可以根据题目描述以及每种方法的题型特征选用合适的特值技巧求解。

行测数量关系神奇方法之“整除”

在行测考试中，利用“整除思想”解题是目前最好用的方法之一。尤其是当题中出现一些明显的文字表述或存在特征数据时，就可以利用整除快速的排除错误答案或者锁定正确答案。接下来，政华教育带大家一起来了解“整除”吧。

什么是“整除”

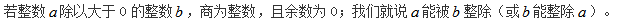考试过程中很多的题目在设置数据时以正整数居多，这就为我们利用“整除”解题提供了有利条件。

什么时候用“整除”

要想用好整除这种方法首先要对一些表述非常的敏感，也就是整除的“暗语”。那么究竟有哪些表述能让我们想到整除并应用整除来解题呢？

1.文字表述：出现整除、倍、平均、每等。

例1：某生产车间有若干名工人，按每4人一组分，多一个人；按每5人一组分，也多一个人；按每6人一组分，还是多一个，该车间至少有多少名工人（）？

A.31 B.41 C.61 D.122

【答案】C【解析】题干描述中出现了“每…人一组”的表述，所以我们可以先来判断一下所求量具备的整除特性。由题意可知，该车间工人数减去1能同时被4、5、6整除，所以结合选项我们不难选出C。

2.数据体现：出现分数、百分数、比例等

例2：林华全家是阅读爱好者，家里有各种书籍，版本也多。已知他家有五分之三的书是中文版的，六分之一是英文版的，八分之一是中英文互译版的，还有多于11本但少于17本是其他版本的。问：他家有多少本英文版书（）？

A.72 B.20 C.15 D.13

【答案】B【解析】题干描述出现分数，优先考虑使用整除特性求解。由题意可知，中英文互译版的数量，则林华家书籍总数能同时被5、6、8整除，所以所求的英文版书的数量×6能被5、8整除，即选项×6能被5、8整除，选B。

例题演练

接下来通过一道例题来感受下“整除”的魅力吧：

例3：某镇政府办公室集中采购一批打印纸，分发给各个职能部门。如果按每个部门4包分发，则多6包；如果按每个部门5包分发，则有1个部门只能分到3包。这批打印纸的数量是：（）

A.38包 B.36包 C.40包 D.42包

【答案】A

解析一：常规思路

假设有x个部门，则根据打印纸总量不变可得方程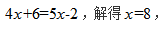：所以打印纸的总数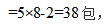选A。

解析二：利用整除巧解题

题目出现了“每……”的表述，所以根据题意可知打印纸总数满足两个条件：①总数减掉6之后，可被4整除；②总数+2之后，可被5整除。下列选项只有A符合条件。故选A。

通过比较发现，整除特性可以辅助我们更加直接判断出所求量的特征，减少大家的计算过程。对于行测考试，时间尤为紧张，这样的方法更能帮大家缩短做题时间，可谓事半功倍。这就是整除的神奇之处！

行测备考“赢在数量”之工程问题

“工程问题”是行测考试数量关系中性价比较高的一类题型，通过合理备考是可以拿到这部分的分数。接下来政华教育带大家一起看看关于工程问题中常考的题型——多者合作。

核心公式

工作总量=工作效率×工作时间

赋值法

1.已知多个主体完工时间，设工作总量为多个时间的最小公倍数，进而表示出他们的工作效率。

2.已知多个效率之间的比例关系时，直接将效率比看成工作效率。

3.已知具体的人或者物的数量时，往往设每个人或者每个物单位时间内的工作量为1。即：直接将人或物的数量，看成工作效率。

例题应用

例1：修一条水渠，甲队独修12天可以完成，乙队独修18天可以完成。现甲独做4天后，剩下的由甲乙合作完成，修这条水渠共得工程款7500元，工程款按量分配，则甲队的工程款多少元（）？

A.2500 B.3500 C.4500 D.5500

【答案】D【解析】设工作总量为36(12和18的最小公倍数)，则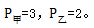干完36份的工作量可得7500元，即1份工作量可得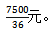36=3×4+(3+2)×t，可得t=4.8天，则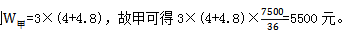

例2：甲、乙两人若共同加工一批零件6天可以完成，若甲、乙两人单独加工，则完成任务所需天数之比为2：3，则乙单独完成任务所需天数比甲多（）天。

A.7 B.5 C.3 D.1

【答案】B【解析】因为W=P×t，当工作总量不变时，工作效率和工作时间成反比，所以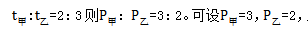那么这项工程的工作总量为(2+3)×6=30.甲单独完成需要30×3=10天，乙单独完成需要30÷2=15天，故乙比甲多5天。

例3：一项工程，在原有工人的基础上，若再加8人，则10天能完成；若再加3人，则20天能完成，现只能增加2人，则完成这项工程需要的天数是（）。

A.20天 B.25天 C.30天 D.32天

【答案】B【解析】已知具体的人的数量，直接设每人每天的工作量为“1”，即人的数量就为工作效率。设原有X人，则该工程工作总量为(X+8)×10=(X+3)×20，可得X=2，工作总量为(2+8)×10=100，根据工作量不变可得100=(2+2)×t，即t=25天。

以上方法希望大家能够认真掌握，并对大家接下来的备考有所帮助！