政华教育

历来，在涉及行测数学运算试题的考试中，排列组合问题往往可以有效考查考生的分析思维能力，深受命题人的喜爱，不断出现于考试中。但是很多考生因为思考角度单一，思维混乱，导致错失“良”分。排列组合题目本质是计数问题，只要明确题目要求我们完成一件什么事以及如何完成这件事情，使用基本的计数思维和原理也是可以得分的。掌握基本知识后，各位考生只要在“如何完成这件事情”的思考上学会多角度思考，题目也就会更简单了。下面政华教育通过例题来感受一下，如何转换视角，以及不同视角思维下，做题的难易程度。

例题

在一张节目表中原有8个节目，若保持原有节目的相对顺序不变，再增加两个节目，求共有多少种安排方法（）？

A.70 B.80 C.90 D.100

【答案】C

【解析】视角一：此题要求在原有8个节目的基础上增加两个节目，可以分为两类情况。一类是：第一步将新加的两个节目相邻，可以把两个节目看成整体有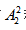种方法，第二步从8个节目形成的9个空隙中选择1个空隙将其插入，有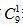种方法，故总的方法数是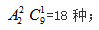另一类是：新加的两个节目互不相邻，从8个节目形成的9个空隙中选择2个空隙将其插入，此种想法就是常规的做法，也是很多考生的习惯做法。

视角二：题目中没有明确说不相邻问题，实质是要将2个新节目插入到已排好节目空隙中，所以完全可以一个一个地加入，首先加入第一个节目，8个节目形成的9个空隙中任选其一有然后再加入第二个节目，前面9个节目已形成的10个空隙中任选其一，有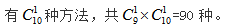种方法，共此视角的关键是要明白每插入一个节目，空隙的总数量会增加一个，空隙的总数量是动态变化的。

视角三：以最终结果为导向，联合实际来看，此题最终结果就是10个节目排好，而其中新加入的两个节目更特殊，所有位置都可能排，所以优先安排这两个节目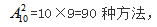，而其他8个位置，只需要将原有8个节目按照规定的顺序填充进去即可。此种想法关键在于结合现实生活实际，以问题结果为导向去思考，题目会变得更容易求解。

通过对该例题三种不同视角下的求解，我们会发现，多转换一些考虑问题的角度，尤其是联系现实生活实际去考虑问题，复杂问题往往会变得容易求解。所以大家在排列组合题目的备考中，不能简单为做题而做题，要更多从不同角度思考，勤加练习，这样做起题目来才会感觉越来越简单！

行测数量关系：巧用排列组合常用方法

在行测考试中，数量关系一直是很多同学比较害怕的专项，因为数量关系除了知识点较多，而且时间也是有限的。其中数量关系最令人头疼的题型莫过于排列组合问题了，很多同学遇到这种类型的题目有时会无从下手。今天政华教育将带领各位同学了解排列组合中最常用的四种方法：优限法、捆绑法、插空法以及间接法。下面政华教育带大家通过例题的形式学习一下。

优限法

题型特征：题干中出现某个或某些特定元素有绝对性的条件要求。

解题思路：我们可以优先考虑有限制条件的元素。在此基础上，再考虑其他元素。

例题：某单位安排五位工作人员在星期一至星期五值班，每人一天且不重复。若甲、乙两人都不能安排星期五值班，则不同的安排法有( )种。

A.6 B.36 C.72 D.120

【答案】C【解析】方法一，考虑星期五有绝对限制条件，星期五不能排甲、乙，所以需要在其他三人中间选择一个在星期五值班，即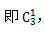剩下的四天四个人没有任何特殊要求，是4个人的全排列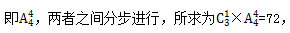，故答案选择C。

方法二，考虑甲乙两人有绝对限制条件，甲、乙不能安排在周五，首先从周一到周四中选择两天安排甲或乙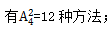，其余三人没有要求，在剩余的日期安排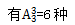，；分步相乘，所求为12×6=72种方法。

捆绑法

题型特征：题干中出现某些元素要求彼此相邻。

解题思路：第一步，将相邻元素捆绑成一个整体；第二步，将这个整体与其他元素进行排序；第三步，最后考虑整体内部各元素间的顺序。

例题：现有2本艺术类、3本教育类和4本医药类书籍需要并排放到同一层书架上，要求同类书籍必须放在一起。问共有多少种可能的放置方式（）？

A.24 B.288 C.1728 D.6912

【答案】C【解析】题目要求同类书籍放在一起，即要求元素相邻。可以采用捆绑法，先把三类书籍分别捆绑成一个整体，然后进行排序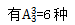，排列。各类书籍内部进行排列分别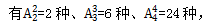所求为6×2×6×24=1728种。故答案选择C。

插空法

题型特征：题干中出现某些元素要求彼此不相邻时。

解题思路：针对此类问题，我们可以先对其他元素进行排列，再将不相邻的元素插入其中。

例题：某学习平台的学习内容由观看视频、阅读文章、收藏分享、论坛交流、考试答题五个部分组成。某学员要先后学完这五个部分，若观看视频和阅读文章不能连续进行，则该学员学习顺序的选择有：（）

A.24种 B.72种 C.96种 D.120种

【答案】B【解析】第一步，先将收藏分享、论坛交流、考试答题三个部分进行排序，有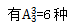学习顺序。第二步，因为观看视频和阅读文章不能连续进行，则将这两个部分插在其他三个部分形成的四个空中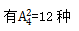，学习顺序。分步运算用乘法，则该学员学习顺序的选择有6×12=72种。故答案选择B。

间接法

题型特征：题干中出现“至少”字眼或从正面情况考虑较为繁杂。

解题思路：所求情况数=总的情况数-反面情况数。

例题：某单位今年新进3个工作人员，可以分配到3个部门，但是每个部门至多只能接收2个人，问共有几种不同的分配方案（）？

A.12 B.16 C.24 D.以上都不对

【答案】C【解析】此题中要求每个部门至多只能接收2个人，如果从正面入手，包括0人、1人、2人，很明显，按照这样的分类进行计算比较麻烦。我们不妨从反面入手，每个部门至多只能接收2个人的反面是这3个人都在同一部门，共有3种可能。而3个人分配到3个部门，若没有要求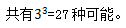，所以所求为27-3=24种可能。故答案选择C。

以上就是排列组合中最常用的四种方法：优限法、捆绑法、插空法和间接法。希望各位同学能够熟记四种方法的题型特征以及解题思路，并在平时多加练习，争取在考试中能够通过题型特征快速联想到解题思路求解，从而选出正确的答案。

行测技巧：排列组合之插空法

众所周知行测数量关系中排列组合一直是公考的重点，而考生在面对排列组合时总是觉得太难，太灵活，很难去把握，今天政华教育就带各位考生来了解应对排列组合的常用方法--插空法，相信各位考生在学习插空法后，应对此类题型就能得心应手。

适用环境：排列组合中某些元素在位置上要求不相邻，不连续，有间隔。

求解思路：先将其他没有要求的元素进行排序，再将要求不相邻的元素插入到其他没有要求的元素形成的空隙中。

例1：甲、乙、丙、丁、戊、五个人排成一队，若甲、乙位置要不相邻，有多少种情况（）？

A.24 B.36 C.72 D.84

【答案】C【解析】甲、乙要求不能相邻，丙、丁、戊无要求；首先可以将丙、丁、戊摆成一排，3个元素3个位置，调换顺序后结果也不同，因此用排列；此时有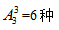站法，排好丙、丁、戊之后再看甲、乙，分步需要用乘法，此时丙、丁、戊内部会形成2个间隔，外加首尾两个空，一共4个空位，既然甲、乙不能相邻，那么将甲、乙插入到丙、丁、戊产生的空位置当中，也就是从4个空位中随机挑2个空位插入甲、乙；这样甲、乙肯定会丙、丁戊、隔开，又因甲、乙所在的位置不同，产生的结果也不一样因此有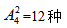排法，故共有6×12=72种，选择C项。

例2：小区内空着一排连续相邻的8个车位，现有4辆车随机停进车位，恰好没有连续空位的停车方式共有多少种（）？

A.48 B.120 C.360 D.1440

【答案】B【解析】4辆车停进8个空车位，肯定有4个车位不停车，现要求空着的停车位没有连续，那可以先将4个车辆先摆成一排，由于车辆肯定互不相同，所以要用到排列，有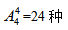停法，停好之后，再将空车位插入到停好车的间隙当中，这样就车辆就不会产生连续，分步用乘法，此时4辆会形成3个间隙，外加首尾两个空位，总共5个空位置，从5个空位置里随机挑4个空位置插入空位，此时空位之间交换顺序对结果无影响，因此用组合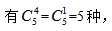，故共有24×5=120种，选择B项。

例3：两对夫妇各带一个小孩乘坐有6个座位的游览车，游览车每排只有1个座位。为安全起见，车的首尾两座一定要坐两位爸爸；两个小孩一定要在不相邻位置。那么，这6人的排座方法有( )。

A.12种 B.24种 C.36种 D.48种

【答案】B【解析】两对夫妇各带一个小孩一共6个人，游览车一共6个座位，每排只有一个座位，也就只能坐一个人，首先爸爸要求坐在首尾，可以先安排爸爸，爸爸之间交换位置对结果有影响，因此有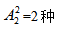方法，再安排其他人，是分步的关系，用乘法，两个小孩不相邻，可以先安排两个妈妈，同理有方法，两个妈妈会形成1个间隙，外加首尾两个空位置，再将两个小孩插入到两个妈妈产生的3个空位置当中，此时两个孩子之间交换顺序对结果有影响，因此用排列，有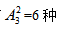方法，分步相乘，共有2×2×6=24种，选择B项。

针对这种方法，相信大家已经完全掌握了，速速去找相关题目练起来吧，在练习的同时，要注意插空法的应用环境：排列组合中某些元素在位置上要求不相邻，不连续，有间隔。注意用排列还是组合要融会贯通喔。

行测数量关系如何科学而巧妙地拿分

无论是国考、省考还是事业单位考试，数量关系一直以来都是较为重要的部分。由于考试时间短，题目较多，再加上很多考生数学基础薄弱，就会选择放弃。但是，近几年公考的人日益增加，竞争越来越大，相差一分可能就会使你与心仪的岗位失之交臂，所以，拿到数量关系的分值就显得尤为重要。另外由于所有题目均是客观的单项选择题，那么结合这个特点就可以运用一些技巧快速解题，接下来政华教育向大家介绍三种较科学且实用的解题技巧。

关联选项

如果题目选项中某两项满足题目中的某个等量关系，那么这两个相关联的选项，极有可能一个是干扰项，一个是正确答案。但有时候，两个选项之间的等量关系，并不明显，需要考生自己去挖掘。

例1：湖北市一小型工厂有5条效率不同的口罩生产线。现接到一批口罩订单生产任务，如果任选3条生产线一起加工，最快需要6天整，最慢需要12天整；5条生产线一起加工，则需要5天整。问如果所有生产线的产能都扩大一倍，任选2条生产线一起加工最多需要多少天完成（）？

A.11 B.13 C.15 D.30

【答案】C【解析】如果产能都扩大一倍，则时间缩短一半。观察选项，发现C选项是D选项的一半，优先推测需要15天完成。

生活常识

万事万物皆相通，问题皆源于生活。其实很多时候，生活常识往往能够帮助我们快速解题。

例2：两同学需托运行李。托运收费标准为10公斤以下6元/公斤，超出10公斤部分每公斤收费标准略低一些。已知甲乙两人托运费分别为109.5元、78元，甲的行李比乙重50%。那么，超出10公斤部分每公斤收费标准比10公斤以内的低了多少元（）？

A.1.5元 B.2.5元 C.3.5元 D.4.5元

【答案】A【解析】由收费标准“略低”一些可知，应该优先选择稍微低一点的。若降低2.5元，已经降低了约50%，不符合略低。

整除特性

若题干存在M=a×b的等量关系，且题干描述中出现平均数、余数、整除等字眼，我们可以结合整除特性快速解题。

例3：2020年受疫情影响，武汉某工厂临时接到一项口罩生产任务，原计划每天生产1000万个，因技术改进，实际每天生产1200万个。结果提前4天完成任务，还多生产800万个，则工厂原计划生产零件( )万个。

A.25200 B.26000 C.28000 D.28800

【答案】C【解析】题干存在工作总量=工作效率×工作时间，并且出现“每”代表平均值，“多”代表余数，优先考虑整除特性。由“每”天生产1000万个可知，零件数是1000的倍数，排除A、D；由“多”生产800万个可知零件数加800是1200的倍数，即加上800后是3的倍数，排除B。

综上所述，数量关系中掌握多种解答技巧，能帮助大家在短时间内科学拿分。同时大家在备考过程中要多做题，提高敏感度，才能熟练运用这些技巧。