行测数量关系难点题目解题技巧
行测考试中这种概率问题真的不要再错了——古典概率之定位法
数量关系一直是行测试卷中大家比较头疼的一类题目。但行测想要拿高分，数量关系题目还是要重点突破的。其中概率问题是考生认为难度较高的题型，因为解题时往往需要用到难度更大的排列组合的相关知识，所以让概率问题看起来“难上加难”。但是有这样一种概率问题，如果能够识别出题型并熟练掌握“定位法”，就能绕开用排列和组合去表示总的等可能样本数和事件A的等可能样本数，直接得出最终结果。下面政华公考就用几道例题带大家一起来看看关于“定位法”的相关知识以及应用。
基本知识
1.定位法的题型特征：题目中对两个元素的相对位置有要求，如两个元素同排、同队、相邻等，可以考虑用定位法。
2.定位法的解题步骤：可以先确定一个元素的位置，再考虑另一个元素的位置可能的样本数(分母)和位置满足题目要求的样本数(分子)。
例题1：一张纸上画了5排共30个格子，每排格子数相同，小王将1个红色和1个绿色棋子随机放入任意一个格子(2个棋子不在同一格子)，则2个棋子在同一排的概率：（ ）
A.不高于15% B.高于15%但低于20%
C.正好为20% D.高于20%
【答案】B【解析】题目要求2个棋子放在同一排，是对这2个棋相对位置有要求，可以用定位法解题。假设红色棋子随机选择某个格子，此时还剩下29个空格子，想再选1个格子放绿色棋子，则共有29个位置可以选，但绿色棋子如果想和红色棋子在同一排，则绿色棋子只能挑选红色棋子所在那一排中剩余5个格子中的一个，故所求的2个棋子在同一排的概率为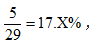
介于15%和20%之间，选择B。
例题2：某学校举行迎新篝火晚会，100名新生随机围坐在篝火四周。其中，小张与小李是同桌，他俩坐在一起的概率为：（ ）
【答案】C【解析】小张和小李2人要坐在一起，是对这两个人相对位置有要求，可以用定位法。假设小张随机选择某个位置，则小李还有99个位置可以选择，其中有小张左、右2个位置可以满足二人相邻，则所求概率为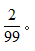
通过以上题目相信大家已经能够基本了解定位法的解题步骤，希望在以后遇到这类题目时，能灵活应用，快速解决此类题目。
持续关注政华公考，教你更多解题技巧。
行测数量关系：利润问题——“买卖中的章法”
“利润问题”在公考中也是常考题型，也是比较好得分的题型，只要我们能够理清楚题干描述的各个概念。利润问题，本质是“买卖”的问题，而“买”“卖”，我们就是要明确买进的情况、卖出的情况，包括买进和卖出的价格、数量，这些都是我们解决利润问题的必要条件。
例1：服装店买进一批童装，按每套获利40%定价，卖出这批童装的80%后，按定价的八折将剩下的童装全部卖出，总利润比预期减少了560元。问服装店买进这批童装花了多少元（ ）？
A.6000 B.8000 C.10000 D.12000
【答案】C【解析】根据题意，实际描述的是购进一批服装分两批卖出去的情况。设买进x元/件，共买进y件。列表如下:
总利润=原利润-560，1.4x×0.8y+1.12x×0.2y-xy=(1.4x-x)×y-560，解得xy=10000，即所求总花费。答案选C。
例2：某超市购进一批水果，按50%的利润定价销售，由于定价比其他超市高，第一天只卖出了总量的10%；第二天打八折促销，卖出了总量的70%；为了尽快售完，第三天超市在第二天的基础上打五折促销，最终全部售完。则这批水果最终：（ ）
A.盈利11% B.亏损11% C.盈利15% D.亏损15%
【答案】A【解析】根据题意，购进水果分三批卖，设购进成本为x元/千克，共购进y千克。整理如下：
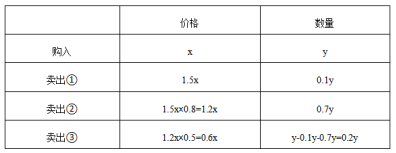
最终所获得的利润率=(总售价-总成本)÷总成本=(1.5x×0.1y+1.2x×0.7y+0.6x×0.2y-xy)÷xy=0.11。答案选A。
例3：商场销售A、B两种成本和定价都相同的商品，A按定价卖出20件后，降价30%卖出40件；B按定价卖出48件后，提价20%卖出12件。商场发现截至此时，销售B商品的利润是销售A商品利润的3倍。则每件A商品的成本是定价的（ ）
A.64% B.68% C.70% D.72%：
【答案】B【解析】根据题意，商场销售A、B两种商品的情况，A、B进价和定价都相同，分别设为x元/件、y元/件我们可以做出整理。
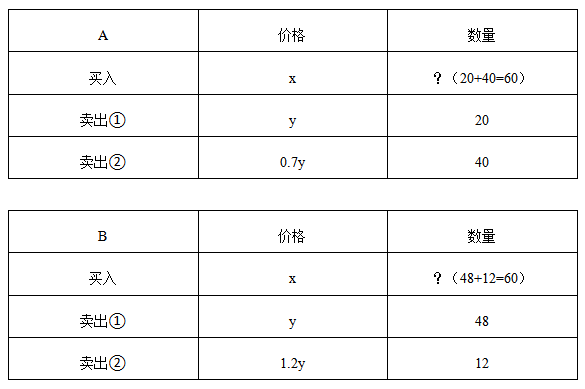
B的利润是A的3倍，可得：48y+1.2y×12-60x=(20y+0.7y×40-60x)×3；化简整理得120x=81.6y，则所求x/y=0.68。答案选B。
总结
利润问题求解，本质就是“买卖”，买入和卖出，列表梳理的方式也能让我们更清晰更直观地梳理出条件来，帮助我们更快地解决问题。当然，掌握利润问题的基本公式也是解决这类问题的前提。
行测数量关系：牢记解题原则，巧解和定最值
和定最值问题是公务员行测考试中的一类常见考点，指的是在几个数加和一定的情况下求其中某个量的最大(小)值的问题。如将20颗糖果分给5个小朋友，求分得糖果最多的小朋友最多分得了多少颗？
解决和定最值问题需遵循一个基本原则：若求其中某个量的最大值，则让其他量尽可能小；若求其中某个量的最小值，则让其他量尽可能大。接下来，政华公考带着这个解题原则一起来求解以下和定最值的常见题型。
1.求最大量的最大值/最小量的最小值
关键点：根据解题原则确定出每一项具体的值，直接相加减即可解题。
例1：6人参加百分制考试，成绩总和为400分，已知6人都及格了，成绩均为整数且依据成绩排名无并列名次，求第一名最多得了多少分（ ）？
A.84 B.90 C.95 D.98
【答案】B【解析】根据解题原则，按照成绩从高到低进行排名，要求第一名最多得了多少分，则其他五人得分尽可能少。已知6人都及格了，则排名第六的人最少为60分，由于无并列名次且都为整数，则排名第五的人最少应比排名第五的人多一分，为61分，排名第四的人得62分，排名第三的人得63分，排名第二的人得64分，排名第一的人为所求量设为x，则x+64+63+62+61+60=330，解得x=84。
2.求最大量的最小值/最小量的最大值
关键点：根据解题原则确定不了具体量的值，可以构造尽可能接近的数列方程求解。
例2：现有40本故事书分给5个人阅读，如果每个人得到的书的数量都不相同，那么得到故事书数量最多的人至少可以得到多少本（ ）？
A.10 B.7 C.9 D.11
【答案】A【解析】根据解题原则，要求得到故事书最多的人最少得了多少本，则其他人所得数量尽可能多。设分得故事书最多的人最少分了x本，由于每个人得到的数量都不相同，则所得故事书数量排名第二的人最多应该比排名第一的少一本，为x-1本，排名第三的人得x-2本，排名第四的人得x-3本，排名第五的人得x-4本，则有x+x-1+x-2+x-3+x-4=40，解得x=10。
3.求中间某个量的最大值/最小值
关键点：可以根据解题原则确定具体量的先确定具体量，其余的构造尽可能接近的数列方程求解。
例3：假设五个相异正整数和为45，则这五个数中排名第三的最大为多少（ ）？
A.7 B.8 C.10 D.13
【答案】D【解析】根据解题原则，按数字大小从多到少进行排列，要求排名第三的数最大为多少，则让其他数尽可能小。由于都是相异的正整数，则排名第五的数最小为1，排名第四的数为2，排名第三的为所求数，设为x，排名第二的数最小应该比排名第三的数大1，为x+1，排名第一的数为x+2，则有x+2+x+1+x+2+1=39，解得x=13。
只要牢记解题原则，就能巧解和定最值问题。更多解题技巧，欢迎关注政华公考！
行测数量关系：空瓶巧换水
在致力于全民环保的21世纪，一些商家为了增强消费者的环保理念，会推广诸如“几个空瓶可以换一瓶水”的活动，由此也衍生出行测中的一个考点—空瓶换水。它是具有技巧性的统筹问题，考查形式相对单一，例如：通过已知的空瓶数量以及兑换原则，让我们去求解可以喝到多少瓶水。很多同学采用的是一步一步兑换的方法，费时且易出错，今天政华公考带大家一起来学习如何巧解此类题目。
例1：某商店为了吸引顾客做一个促销活动，每3个空汽水瓶可以换一瓶汽水，问：小张共有11个空瓶最多可以喝到几瓶汽水（ ）？
解析：(1)基本方法：由于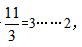
可知能换到3瓶汽水还剩2个空瓶，3瓶汽水喝掉后再加剩余的2个空瓶，可得到5个空瓶。
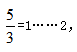能换到1瓶汽水还剩2个空瓶，1瓶汽水喝掉可得到3个空瓶，又能换到1瓶汽水，最终共喝到3+1+1=5瓶汽水。
(2)巧解方法：明确题目中的核心兑换规则，3个空瓶换1瓶汽水，也就是3空瓶=1瓶水=1空瓶+1份水，即2空瓶=1份水。因此，直接用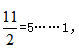
最多能喝到5瓶汽水。
【解题方法】直接套用公式——已知规则及空瓶数，问最多能喝到水的瓶数。
例2：若12个空瓶可以免费换1瓶汽水，现有101个空瓶，最多可以免费喝到几瓶汽水（ ）？
A.8瓶 B.9瓶 C.10瓶 D.11瓶
【答案】B【解析】明确题目中的兑换规则，12个空瓶换1瓶水，即12空瓶=1瓶水=1空瓶+1份水，即11空瓶=1份水。因此所求为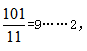
最多能喝到9瓶汽水。
例3：商店开展“7个空瓶换一瓶啤酒”的优惠活动。已知张先生在活动促销期间共喝掉347瓶“红星”啤酒，问张先生最少买多少瓶啤酒（ ）？
A.296 B.298 C.300 D.302
【答案】B【解析】明确题目中的兑换规则，7空瓶=1瓶酒=1空瓶+1份啤酒，即6空瓶=1份啤酒。此时设张先生最少需要买x瓶啤酒，则换回酒的份数为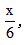
由题可得：
此时需要分析x的取值，x假设为最少，而啤酒的瓶数一定是整数，需要向上取整，因此最少需要买298瓶啤酒，故选择B选项。
【解题方法】间接套用公式——已知规则及喝到水的份数，求至少应买多少瓶水。
以上即为空瓶换水的巧解方法。以后解决此类问题时，首先需要明确题目中的兑换规则，将兑换规则转化为a空瓶=b份水的形式，再进行求解即可。此类问题在考试中的考查形式相对来讲比较单一，同学们只要明确方法，相信可以轻松解决。
行测数量关系典型题型：牛吃草问题
行测数量关系问题对大部分考生来说都是一个比较头疼的问题，计算量大，耗时长。那么，怎么在有效时间内快速解决问题呢？今天政华公考就来介绍一下比较经典的牛吃草问题的答题技巧，希望能够对大家有所帮助。
题型特征
一个典型的牛放牧问题的条件是：假设草在持续生长，且生长速度固定，不同数量的牛吃掉同一片草地所需的天数不同，求几头牛可以吃掉这片草地需要多少天。由于吃的天数不同，草每天都在生长，因此草的存量随着吃的天数不断变化。
牛群放牧问题的关键在于，这一问题具有隐蔽性。如果每头牛每天以不同的速度和数量吃草，这个问题就没有解决办法。因此，为了确定这一问题，每头牛每天吃草的速度和数量必须相同。
核心公式
原有草量=(牛每天吃掉的草量-每天生长的草量)×天数
基本思路：假设每一头牛的吃草速度为1，根据不同的牛吃草列出关于总草量的等量关系式，进而求出我们求的数值。
解题方法
例1：牧场上一片青草，每天牧草都匀速生长。这片牧草可供10头牛吃20天，或者可供15头牛吃10天。问：可供25头牛吃几天（ ）？
A.2 B.3 C.4 D.5
【答案】D【解析】设每头牛吃1份草，每天新增加的牧草为x，可供25头牛吃t天。根据核心公式可得：(10-x)×20=(15-x)×10=(25-x)×t，解得t=5，所以答案选D。
例2：某水库共有10个泄洪闸，当10个泄洪闸全部打开时，8小时可将水位由警戒水位降至安全水位；只打开6个泄洪闸时，这个过程为24小时，如水库每小时的入库量稳定，问如果打开8个泄洪闸时，需要多少个小时可将水位降至安全水位（ ）？
A.10 B.12 C.14 D.16
【答案】B【解析】某水库原有水量相当于原有草量，泄洪闸相当于牛，假设1个泄洪闸的泄水量为1，水库每小时的入库量为x。则由牛吃草核心公式可得：(10-x)×8=(6-x)×24=(8-x)×t，解得t=12，故选B。
牛吃草的困难在于草每天都在生长，因此草的数量在不断变化。因此，解决这些问题的关键是找到一种方法，从变化中找到恒定的数量，例如单位时间内每头牛的草速和原始草量。
牛吃草是一种难度相对适中的题型，大部分题目可能会以不同的形式表现出来，例如例题2水库放水等，但是整体换汤不换药。只要理解题目含义，掌握核心公式，找到对应的量，利用核心解题方法，就能解决问题、从容应对。在我们行测考试中，这种解题技巧还有很多，只要掌握之后便能够更好地应对考试。
