政华教育

第二道题，重点是要保证抽到两张相同花色的牌，第一张可以随便抽，假设是梅花；第二张也是梅花就可以了，然而我们并不能保证，可能抽到其他三种花色，比如第二张抽到的是方块；若第二张抽到方块，则第三张只要抽到前面两种花色的牌就可以了，然而依然不能保证，第三张可能抽到黑桃，第四张依然不能保证抽到你理想的三种花色，可能抽到了红桃。在这样的情况下，就需要抽第五张，第五张不论是哪种花色，由于手中四种花色都已经抽到了，则都可以保证跟前面四张牌中的某一张凑成两张相同花色的牌。这种总是离心中所求差一点的情况，就是宛若非酋的最不利了，也是大家在考试中经常会遇到的一种题型。

二、“非酋”的特征及其破解原则

特征：题干中出现“至少……保证……”

破解原则：找到离成功差一点的所有情况，最后在此基础上+1。式子表示为：最不利情况数+1。

三、“非酋”的高光时刻

例1：有软件设计专业学生90人、市场营销专业学生80人、财务管理专业学生20人及人力资源管理专业学生16人参加求职招聘会，问至少有多少人找到工作就一定保证有30名找到工作的人专业相同？（）

A.59 B.75 C.79 D.95

【答案】D【解析】问题出现“至少……保证……”，这就是“非酋”出没的标志。想成功的目标是30名专业相同，离成功差一点就是有29名专业相同，就差那么1名。考虑最不利的情况，即财务管理专业的20名学生和人力资源管理专业的16名学生全部找到工作，然后软件设计专业和市场营销专业的学生各有29名找到工作，此时再有1名学生找到工作，就能保证有30名找到工作的人专业相同，则至少需20+16+29+29+1=95名学生。答案选D。

例2：箱子里有大小相同的3种颜色玻璃珠各若干颗，每次从中摸出3颗为一组，问至少要摸出多少组，才能保证至少有2组玻璃珠的颜色组合是一样的？（）

A.11 B.15 C.18 D.21

【答案】A【解析】题目要求颜色组合一样，那么我们就要知道一共有多少种组合，我们可以按照颜色种类数来进行划分，摸出的3颗玻璃珠只有一种颜色，有3种情况；有两种颜色，有有三种颜色，有1种情况。故共有10种不同的颜色组合。考虑最不利原则，10种颜色组合各取一组，此时再取1组的话，就一定能保证与前面的某组颜色组合一样，则至少需要10+1=11组就能保证一定有两组玻璃珠的颜色组合一样。

最不利原则题目特征明显，解题过程就犹如大家的备考之旅，只要不放弃，经历过重重困难之后，再迈出最后一步，总能达成所愿。大家在后面的学习过程中还是要多多练习，感受“非酋”的高光时刻。

行测数量关系技巧：整除法解计算问题

数量关系一直是行测题目中考生公认的难点，多数人一度头疼到放弃，但此部分又在国、省考中占分较多，放弃很有可能会影响考试，因此想要在短时间内理清题目，找到解题方法，选出正确答案至关重要，而整除法在数量关系的考试中往往能助我们一臂之力，也能帮助考生多拿分数。

在历年试题中，多数计算问题虽说只需要根据题干描述列出方程再解方程即可，但往往会有考生在题目分析过程中不能准确地列出方程，或者在解方程时花费大量时间。然而有一部分题目如果我们能够识别出一些特征表述，就可以快速选出正确答案或者排除错误选项，这就是接下来要给大家介绍的整除法。整除法是指通过题目中描述的整除特性来解题的方法。首先，什么是整除特性呢？比如：男生人数和女生人数的比是3：5，这句话中给出男女人数的比例关系，可以理解为男女人数分别为三份和五份，由于人数一定是整数，所以男生人数一定是3的倍数，即能够被3整除。同理，女生人数就能够被5整除。接下来，我们通过几道例题具体了解一下整除法的应用。

例1：某班级发放课外书，平均每人能分到7本。后来该班级又转来若干学生，这样每人能分到6本，该班级课外书总数是( )。

A.180 B.210 C.240 D.280

【答案】B【解析】由题意可得课外书总数=7×班级原人数=6×班级现人数，则课外书总数是7和6的倍数，选项中只有B符合。

例2：甲、乙、丙、丁四个工厂共有100名高级技工。其中甲、乙两个工厂的高级技工数量比是12：25，丙工厂的高级技工人数比丁工厂少4人。问丁工厂的高级技工人数比甲工厂：( )。

A.多6人 B.少6人 C.多9人 D.少9人

【答案】D【解析】用甲、乙、丙、丁分别表示四个工厂的高级技工人数，由题意可知，甲：乙=12：25，则甲+乙的总人数是37的整数倍，则甲+乙=37或74。若甲+乙=37，则丙+丁=100-37=63，又因为丙=丁-4，此时丙、丁为非整数，排除。故甲+乙=74，即甲=24，又因丙+丁=100-74=26，丙=丁-4，可得丁=15，故丁工厂的高级技工人数比甲工厂少24-15=9人。

除了上述题目之外还有很多题目也可以用整除法，在这里给大家总结一下整除法的适用环境：一般分为两种情况，第一种：文字体现，比如题目中出现平均、每、整除、倍数等时，第二种：数据体现，比如题目中出现分数、比例、百分数等时均可以优先考虑整除法。

同时为了快速选出哪一个选项满足整除特性，我们也需掌握常见小数字的整除判定，在这里给大家罗列出来：

1.依据末n位判定数字是否能被2.5整除。

2.依据各位数字之和判定数字是否能被3.9整除。

3.依据若数字为三位数及以下直接除，三位数以上从后往前数三位后划线，大数减小数的差判定数字是否能被7整除。

4.依据奇数位上数字和与偶数位上数字和之差判定数字是否能够被11整除。

整体来看整除法简单易上手，能够在一部分题目中帮助我们省去列式计算的过程快速确定答案，各位考生只需熟悉适用环境和常见小数字的整除判定，多加练习即可掌握。

行测数量关系：带你轻松踢开平面几何的三个“绊脚石”

平面几何问题，在行测数学运算这一部分可以说是常青树，但是对于广大考生来说平面几何却成为绊脚石。通常大家做平面几何题目感受是：意难懂、图难画、题难解。为了帮助大家解决做题中遇到的困难，下面政华公考为大家整理平面几何的三个要点。

要点一：真知灼见，应万变→基本公式

例1：一个圆形，半径变为原来的4倍之后的圆的面积，等于半径增加2厘米之后的面积的4倍，则原来的半径是（）？

A.1厘米 B.2厘米 C.3厘米 D.4厘米

【答案】B【解析】根据题干描述，半径变为原来4倍时圆的面积=半径增加2厘米时圆面积×4；设圆原来半径为r，代入圆形面积公式可得出方程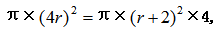：解得r=2，正确答案B。

要点二：火眼金睛，识初见→相似三角形

1.相似三角形对应角相等，对应边成比例。

2.相似三角形面积比等于相似比的平方。

例2：

将一块三角形的绿地沿一条直线分成两个区域，一为三角形，一为梯形，已知分出的三角形区域的面积为1.2亩，梯形区域的上、下底分别为80米、240米，问分出的梯形区域的面积为多少亩？（）

A.9.6 B.8.9 C.8.8 D.7.6

【答案】A【解析】根据题干描述，△AEF相似于△ABC，相似比为EF：BC=80：240=1：3；面积比为相似比的平方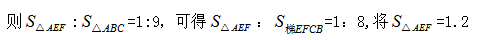，亩代入得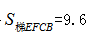亩故正确答案A。

要点三：雾里探花，来构建→解直角三角形

1.勾股定理：在直角三角形中两直角边的平方和等于斜边的平方。

2.常见的勾股数(3.4.5)；(6.8、10)；(5.12.13)……

3.特殊角度直角三角形三边关系：含30度直角三角形三边比例关系

例3：一艘非法渔船作业时发现其正右方有海上执行船，于是沿下图所示方向左转30度后立即以15节(1节=1海里/时)的速度逃跑，同时执法船沿某一方直线方向匀速追赶，并正好在某一点追上。已知渔船在被追上时逃跑的距离刚好与其发现执法船时与执法船的距离相同，则执法船的速度为多少节（）？

【答案】D】【解析】据题干描述画出图形，如下：

A为渔船逃跑起点、B为执法船起点、C为追上的位置。根据渔船在被追上时逃跑的距离刚好与其发现执法船时与执法船的距离相同，有AB=AC，则△ABC为等腰三角形，且∠过A点做辅助线AD垂直于BC，故△CAD和△BAD为2，D为中点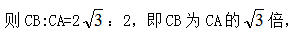，两船运动时间相同，则执法船的速度也为渔船的正确答案D。

大家在做平面几何类问题，首先要牢记公式，以不变应万变；其次要能够识别出题目图形中隐含的相似三角形；最后，个别题目需要做辅助线构造直角三角形，后期还需大家多加练习，让绊脚石成为我们前进路上的垫脚石。

行测指点：行程问题之相遇与追及模型

公考的行测考试中，最令人头疼的莫过于数量关系了。数量关系的相关考题以变化莫测著称，其中的行程问题在数量关系中也时常出现，每年都使许多考生焦头烂额。行程问题虽难，但其中的一类经典题型——相遇与追及，因为有具体的模型、公式，故而成为大家可以通过针对性学习，进而完全掌握的一类题型。今天政华公考就带大家一起学习直线上的相遇与追及问题。

直线上的相遇问题

基本公式：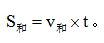

注：t必须是相遇的运动主体同时运动的时间。

例题：小车、客车从甲地开往乙地，货车从乙地开往甲地，它们同时出发，货车与小车相遇20分钟后又遇客车。已知小车、货车和客车的速度分别为75千米/时、60千米/时和50千米/时，则甲、乙两地的距离是：（）

A.205千米 B.203千米 C.201千米 D.198千米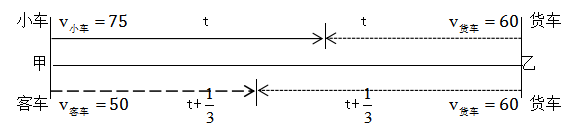

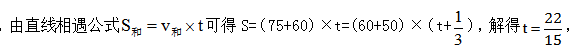【答案】D【解析】题中描述的是货车分别与小车、客车相遇的过程(如上图)。设小车与货车相遇的时间为t，则客车与货车相遇的时间为根据图中路程间的等量关系，则甲、乙两地的距离是故本题选D。

直线上的追及问题

基本公式：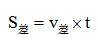

注：t必须是追及的运动主体同时运动的时间。

例题：甲以每小时6千米的速度步行从A地前往B地，在甲出发90分钟时，乙发现甲落下了重要物品，立即骑自行车以每小时12千米的速度追甲，终于在上午11点追上了甲。问甲出发时间是上午几点？（）

A.7 B.8 C.9 D.10

【答案】B【解析】甲从A点出发90分钟即1.5小时后到达C点，此时甲乙之间的距离为6×1.5=9千米，此时甲从C、乙从A同时出发，到D点乙追上甲(运动时间相等)，设乙从出发到追上甲的时间为t，由直线追及公式故9=(12-6)×t，解得t=1.5，所以甲在11-1.5-1.5=8点出发。故本题选B。

学以致用

例题：某人乘坐公交车，公交车的速度是60km/h，下车10分钟后发现遗漏了物品，马上改乘出租车追赶，出租车的速度是85km/h，出租车起步是8元(含4km)，超出为后1.5元/km，问出租车的车费是多少元？（）

A.40 B.46 C.48 D.53

【答案】D【解析】A点下车后，公交车又走10分钟即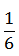小时后到达B点，此时公交车与人之间的距离为60×=10千米。此时某人乘出租车从A、公交车从B同时出发，到C点出租车追上公交车(运动时间相等)，设出租车追公交车的时间为t，由直线追及公式故10=(85-60)×t，求得t=0.4，出租车所走的路程为85×0.4=34千米，车费为(34-4)×1.5+8=53元。故本题选D。

以上就是关于行程问题中直线上相遇与追及模型的基本公式。在解题的时候，大家只需要通过绘制并观察行程图，套用公式求解即可。在此基础上如果能加入自己的理解，举一反三，提炼出属于自己的方法技巧，就能把此类题目完美拿下。同时也要注意，不管是相遇还是追及问题，公式中的时间都是同时运动的时间。政华公考建议大家备考期间勤加练习，熟练掌握直线上的相遇与追及模型。

行测技巧：牛吃草问题的常见模型

在公职考试中行测考试因涉及题型多、考试时间紧，往往让考生头疼不已，因此行测复习的重点就是尽可能地掌握特征明显、模型固定、掌握技巧方法后比较容易拿分的题型。接下来政华公考带大家学习行测数量关系中的这样一种题型——牛吃草问题。

题型特征

1.题干中存在排比结构。

2.初始量(初始草量)固定不变。

3.总量(青草总量)受两个因素(牛和草)的影响。

核心公式

牛吃草过程中牛不管以怎样的方式去吃，初始草量都是一样的，利用这一特点分析可得：初始草量=(牛每天的吃草量-草的生长速度)×天数

模型介绍

1.追及——草在生长

例1：牧场上一片青草，每天生长的草量一样。这片草地可供10头牛吃20天，可供15头牛吃10天，那么可供25头牛吃几天呢？（）

A.3 B.5 C.7 D.9

【解析】答案选B。题干中出现排比结构，初始草量不变，青草总量受牛和草两个因素的影响，符合牛吃草问题的特征，且这两个因素影响青草总量的方向不一致，一个使青草总量变少，一个青草总量变多，这类题型属于牛吃草问题中的追及问题。典型特征是“草均速生长”。

假设每天草的生长速度为X，每头牛每天吃草量为1，则25头牛吃时可供T天，结合牛吃草的核心公式初始草量=(牛每天的吃草量-草的生长速度)×天数，可以列出式子由左边这个等式可以求出X=5，再代入右边等式可求出T=5，因此选择B。

2.相遇——草在枯萎

例2：受天气影响，某片草地的草每天都在以相同的速度枯萎。已知这片草地上的草可供24头牛吃4天，可供9头牛吃8天，照此计算，可供多少头牛吃10天（）？

A.4 B.5 C.6 D.7

【答案】C【解析】题干中出现排比机构且青草总量受牛和草两个因素的影响，符合牛吃草问题的特征，且这两个因素影响青草总量的方向一致，均使青草总量变少，这类题型属于牛吃草问题中的相遇问题。典型特征是“草均速枯萎”。

假设每天草的生长速度为X，每头牛每天吃草量为1，则可供Y头牛吃10天，结合核心公式，可列式为由左边等式可求出X=6，再代入右边等式可求出Y=6，因此选择C。

3.极值型——草吃不完，放养牛最多

例3：有一片牧场，每天草会按一定量生长。这片牧场可供27头牛吃6天，或23头牛吃9天。受到政策影响，为保护这片草地永远不被吃完，那么最多可以放几头牛吃草（）？

A.13 B.15 C.17 D.19

【答案】B【解析】题干中出现排比结构且青草总量受牛和草两个因素的影响，符合牛吃草问题的特征，且这两个因素影响青草总量的方向不一致，一个使青草总量变少，一个青草总量变多，属于追及情况。在此基础上将问法改为求“草不被吃完的情况下，最多放养的牛的数量”则属于极值型牛吃草问题。

假设每天生长的草量为X，每头牛每天吃草量为1，结合核心公式，可列式为即每天草的生长量为15，如果要保证草地永远不被吃完，那么每天牛吃的草量就不得大于每天草的生长量，最多则是等于每天草的生长量，所以最多可以放15头牛，因此选择B。

以上就是牛吃草问题常见的3种模型，大家只要能识别各类模型的特征，再结合解题核心公式，基本上就可以“拿捏”牛吃草问题。政华公考希望本次分享能够帮助到大家！