政华教育

【答案】C【解析】题目最终的目标是想要有6张牌的花色相同，考虑最不利的情况，就是先不让同一种花色抽出6张牌，每种花色最多先抽5张牌，还有大小王(无花色)，此时已经抽出了4×5+2=22张牌，未达成目标。但接下来再抽出一张牌，不管抽出的是什么花色，该种花色的牌已经有6张牌了，即达成了目标。所以至少抽出的牌数为22+1=23张牌，选择C选项。

【总结】最不利数=目标数-1，想要有10张花色相同的牌，每种花色最多先给10-1=9张；想要有7张点数相同的牌，每种点数最多先给6张。

练一练

例题：某高校举办的一次读书会共有37位学生报名参加，其中中文、历史、哲学专业各有10位学生报名参加了此次读书会，另外还有4位化学专业学生和3位物理专业的学生也报名参加了此次读书会，那么一次至少选出几位学生，将能保证选出的学生中至少有5位学生是同一专业的？（）

A.17 B.20 C.19 D.39

【答案】B【解析】想要达成的目标是保证至少有5位学生是同一专业的，按照：最不利数=目标数-1，每个专业最多先选4人，其中中文、历史、哲学专业各有10位学生，先各选4人，化学专业共4人，全选出来，物理专业有3位同学，最多选3人，已经选出了4×4+3=19人，接下来再选一个人，一定中文、历史、哲学三个专业其中的一个，则该专业选出的人数为5，满足条件，本题选B。

通过上述讲解，政华公考相信大家对最不利原则的问题有了一定的了解，同学们要牢记题型特征和解题方法，多加练习，掌握这种相对简单的题目。

行测数量关系：如何破解古典概率

古典概率在行测数量关系中是一种常考的题型，很多同学拿到这类题目，往往比较头疼，做题比较慢，一方面是因为做题思路不明确，同时难以确定总事件和A事件，另一方面是因为在计算总事件和A事件的样本数时需要用到排列组合的知识，而很多同学遇到排列组合又会望而却步。基于以上两方面的原因就导致很多同学做这类型题目的时候，时间长，正确率低。接下来就由政华公考结合例题带大家一起学习一下如何快速地解决古典概率问题。

基本公式

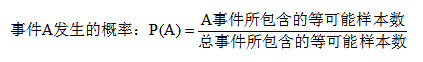
典型例题

例1：某公司将在本周一至周日连续七天举办联谊会，某员工随机选择其中连续的两天参加联谊会，那么他在周五至周日期间连续两天参加联谊会的概率为：（）

【答案】B【解析】根据题意，总事件是员工从周一至周日中选择连续两天参加联谊会，根据枚举法，对应的样本数为6；A事件是员工从周五至周日中选择连续两天参加联谊会，对应的样本数为2，则所求概率为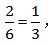故本题选B。

【总结】解决古典概率问题的思路是先找出总事件和A事件分别是什么，再计算出各自所对应的等可能样本数，最后结合公式进行求解。

例2：已知一个箱子中装有12件产品，其中2件次品。若从箱子中随机抽取2件产品进行检验，则恰好抽到1件次品的概率是：（）

【答案】B【解析】根据题意，总事件是从12件产品中任意抽取2件，此时若用枚举法所对应的样本数较多，花费时间较长，故采用组合数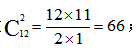A事件是恰好抽到1件次品，即抽取的两件产品1件次品，1件非次品，对应的样本数为

例3：小明有2盆兰花和3盆杜鹃，小明打算随机拿出2盆送给小红，则至少有1盆兰花的概率是：（）

【答案】D【解析】根据题意，总事件是从2盆兰花和3盆杜鹃中任意选2盆花，对应的样本数为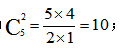A事件是选择的两盆花中至少有一盆是兰花，其中包括两类情况，一类是1盆兰花1盆杜鹃，对应的样本数为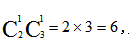另一类是两盆都是兰花，对应的样本数为1，所以A事件的样本数为6+1=7，则所求概率为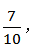故本题选D。

通过上面三道例题的练习，政华公考相信大家对于古典概率问题的解题方法也有了一定的认识，为了进一步熟练这种题型，还需要同学们在备考中勤加练习，熟练之后才可以在考场上应用自如，帮助我们提高做题的速度。

行测数量关系：利用隔板巧解同素分堆问题

排列组合问题作为行测考试中的一个考点，难度系数很高，是令很多同学耗费精神的一个知识点，但是排列组合类的题型中，不乏有一些比较特殊的题型，可以通过特殊的思维进行解决。那么今天政华公考就带大家来通过隔板思维解决相同元素的分堆问题。

例1：有10个相同的苹果，分给3个小朋友，每个小朋友至少一个，问共有多少种分法？（）

A.45 B.36 C.120 D.42

【答案】B【解析】根据题意，10个相同的苹果分给3个小朋友，也就是把苹果分成3堆。那么将10个苹果排开，只需要往苹果与苹果的空隙之间插入2块板，就可以分为3堆。因为每个小朋友至少一个，所以只能在10个苹果中间的9个空隙中插入2块板，因为空与空之间是相同的，改变顺序对结果没影响，用组合数，答案为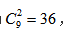所以答案选择B。

上述例题就是一个简单的“隔板法解决同素分堆”的题目，就是将相同的东西分给几个人，我们在东西的中间空隙用板子隔开进行分堆即可，接下来一起来总结一下可以用隔板法解题的题型特征以及解题公式。

题型特征：把n个相同元素分给m个不同的对象，每个对象至少1个元素，问有多少种不同分法的问题。1.所要分配的元素必须完全相同(例如10个相同的苹果)。2.每个对象至少分到1个(比如每个小朋友至少一个)。

解题公式：方法数共有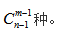

了解题型特征以及公式后，那我们来看看怎么来灵活地运用“隔板法”呢？

例2：把10个相同的苹果分给3个小朋友，每个小朋友至少2个，问共有几种分法？（）

A.15 B.21 C.20 D.42

【答案】A【解析】根据题目，“10个相同的苹果”说明相同元素，“分给3个小朋友”说明要分成3堆，但是题目中是“每个小朋友至少2个”，与题型特征中“每个对象至少1个”不符，不能直接使用“隔板法”，所以我们要先把“至少2个”变为“至少1个”。如果先给每个小朋友发1个苹果，现在苹果还剩10-3=7个，7个相同分发给3个小朋友，每个小朋友至少1个，直接使用公式，答案为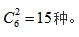选择A。

相信大家通过上述题目的讲解，能对“隔板法”有一定的了解。政华公考建议大家在备考期间需多多练习，真正做到熟练掌握这类问题，希望对于大家的备考能有所帮助。

行测排列组合别放弃，隔板模型拯救你

排列组合问题一直是行测数量关系考查的重点，其题型灵活多变，整体难度较大，让很多考生望而却步，很多考生的感觉是考试年年考，但与“我”无关。真的是这样的吗？排列组合问题就真的不可突破了吗？难道我们也要和对手一样放弃了吗？其实不然，排列组合也有很多简单的、可掌握的知识点，今天政华公考就带大家来学一学其中的一个题型——隔板模型。

初识隔板模型

例题：某城市一条道路上有4个十字路口，每个十字路口至少有1名交通协管员，现将8个协管员名额分配到这4个路口，则每个路口协管员名额的分配方案有：（）

A.35种 B.70种 C.96种 D.114种

【答案】A【解析】题干要求将8个协管员名额分配在4个不同的十字路口，每个路口至少1名交通协管员。根据题干被分配的是协管员名额，名额不存在差异，可以看成同样的元素；要求分配给的是4个十字路口，每一个路口是不一样的，可以看成是分给不同的对象；且题干要求每个路口至少一个。所以可以抽象为将8个相同元素分配给4个不同对象，每个对象至少分配1个元素，如下图：

此时只需要将8个相同元素的间隔上插入3个隔板，即可以将8个相同元素按照不同数量分配给了4个不同对象。

如按照以上的方式插入隔板的话相当于A分2个元素，B和C分1个元素，D分4个元素。随着隔板所选的3个间隔的不同，产生不同的数量分配，但是每一个对象至少要分1个，只能在中间的7个间隔里选3个插入隔板。则总方法数应为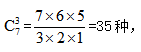故选A选项。

【技巧点拨】把n个相同的元素分给m个不同的对象，每个对象至少分1个元素，则可以理解为隔板模型类的题目。其方法数为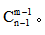

变形突破

如果将n个相同元素分配给m个不同对象，每个对象至少为1个元素，直接带模型及结论即可，但是在考试过程中，我们往往就会遇到一些变形，我们一起来学习一下吧。

变形一

例题：某城市一条道路上有4个十字路口，每个十字路口至少有2名交通协管员，现将13个协管员名额分配到这4个路口，则每个路口协管员名额的分配方案有：（）

A.28 B.56 C.72 D.112

【答案】B【解析】题干要求将13个相同的名额分配在4个不同的十字路口，每个路口至少2个。题干依然是将n个相同元素分给m个不同对象的题目，只是要求变为了每个对象至少分2个元素。此时我们可以考虑先给每个对象先分1个元素，则就能转化成每个对象至少1个的模型。相当于将13-4=9个相同元素分给4个不同对象，每个对象至少分1个，即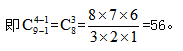

【技巧点拨】把n个相同的元素分给m个不同的对象，每个对象至少分多个元素时，先转化成每个对象至少分1个的模型，再利用隔板模型进行求解。

变形二

例题：某城市一条道路上有4个十字路口，现将8个协管员名额分配到这4个路口，则每个路口协管员名额的分配方案有：（）

A.87种 B.112种 C.165种 D.360种

【答案】C【解析】题干要求将8个相同的名额分配给4个不同的十字路口，每个路口的名额没有要求，即有些路口可以分不到。题干依然是将n个相同元素分给m个不同对象的题目，只是要求变为了每个对象可以分不到(分0个)元素。此时我们可以考虑先向每个对象先“借”1个元素，则每一个对象至少需要将“借”的还回去，就转化成了每个对象至少1个元素的模型。相当于将8+4=12个不同的元素分给4个不同的对象，每个对象至少分1个元素，即有故选C选项。

【技巧点拨】把n个相同的元素分给m个不同的对象，存在某个对象可能分不到(分0个)元素。则可先向该对象先“借”1个元素，然后即可转换为每个对象至少分1个的模型，再利用隔板模型进行求解。

以上即为隔板模型的标准型及其两个变式，它本质上就是相同元素的分配问题，事实上，我们只需要记住并且理解标准型的定义和结论，变式题型可举一反三，通过先分或先借的方法转换使其满足每个对象至少分1个元素的条件，再代入公式计算即可。所以排列组合也有可做的题目，不能全然放弃哦！

行测数量关系：如何应对一元二次函数求极值

提到与一元二次函数相关的问题小伙伴们是不是倒吸了一口冷气呢？大家第一反应可能想到的都是复杂的求根公式，觉得这类题目计算量大不好求解。但是一元二次函数求极值作为行测考试中经常会出现的一类题目，究竟有没有简单有效的方法去解决呢？今天政华公考就带着小伙伴们一探究竟！

知识铺垫

一般式：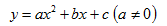

函数图像及两根：其图像是一条关于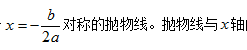的两个交点分别记为

开口方向与极值：抛物线的开口方向由a的正负决定，当a>0时，抛物线开口向上，则函数在对称轴处存在最小值；当a<0时，抛物线开口向下，则函数在对称轴处存在最大值。

考查形式以及解决方法

1.考查形式

一元二次函数在考试当中经常会结合利润问题以求极值的形式出现。

2.解决方法

因为函数图像的对称性，所以往往可以将一般式整理为两项相乘的形式，也就是零点式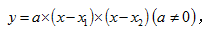令这两项各自为0，并计算出函数式为0时的两个根，由于图像对称的这一性质，该平均值位于对称轴上时，可以使得一元二次函数求得最值。

例题展示

例1：某商品的进货单价为80元，销售单价为100元，每天可售出120件。已知销售单价每降低1元，每天可多售出20件。若要实现该商品的销售利润最大化，则销售单价应降低的金额是：（）

A.5元 B.6元 C.7元 D.8元

【答案】C【解析】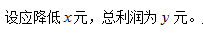则降低后的销售单价为(100-x)元，销量为(120+20x)件，进货单价为80元，则总利润y=(100-x-80)×(120+20x)，y=0时的两个根为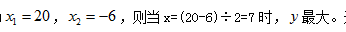选择C选项。

例2：某苗木公司准备出售一批苗木，如果每株以4元出售，可卖出20万株，若苗木单价每提高0.4元，就会少卖10000株。那么，在最佳定价的情况下，该公司最大收入是多少万元？（）

A.60 B.80 C.90 D.100

【答案】C【解析】设苗木单价提高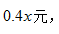则可卖出(20-x)万株，此时收入为y万元，y=(4+0.4x)×(20-x)，令y=0，可解得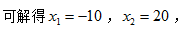则当x=(-10+20)÷2=5时，y取最大值，收入最大为(4+0.4×5)×(20-5)=90万元。选择C选项。

【点拨】

今天的小知识你收下了吗？其实一元二次函数的相关问题并没有大家想得那么复杂，只要大家掌握核心关系，勤加练习，一定能有所收获。希望大家能够在政华公考的帮助下节省宝贵的时间呦！